2023年苏科版数学八年级下册全方位训练卷8.3频率与概率

更新时间：2023-02-08 浏览次数：54 类型：同步测试

一、单选题（每题3分，共24分）

1. 若气象部门预报明天下雨的概率是70%，下列说法正确的是（）

A . 明天下雨的可能性比较大 B . 明天下雨的可能性比较小 C . 明天一定会下雨 D . 明天一定不会下雨

答案解析收藏纠错 + 选题
2. 下列说法不正确的是（）

A . 不可能事件发生的概率是0 B . 概率很小的事件不可能发生 C . 必然事件发生的概率是1 D . 随机事件发生的概率介于0和1之间

答案解析收藏纠错 + 选题
3. (2023七下·青岛期末) 小明做“用频率估计概率”的实验时，根据统计结果，绘制了如图所示的折线统计图，则符合这一结果的实验最有可能的是（）

A . 抛掷一枚硬币，落地后硬币正面朝上 B . 一副去掉大小王的扑克牌，洗匀后，从中任抽一张牌的花色是红桃 C . 抛一个质地均匀的正方体骰子，朝上的面点数是3 D . 在“石头、剪刀、布”的游戏中，小刚随机出的是“石头”

答案解析收藏纠错 + 选题

4. (2022七下·新城期末) 王师傅对某批零件的质量进行了随机抽查，并将抽查结果绘制成如下表格，请你根据表格估计，若从该批零件中任取一个，为合格零件的概率为（）

随机抽取的零件个数 $\text{[math]}$	20	50	100	500	1000
合格的零件个数 $\text{[math]}$	18	46	91	450	900
零件的合格率 $\text{[math]}$	0.9	0.92	0.91	0.9	0.9

A . 0.9 B . 0.8 C . 0.5 D . 0.1

答案解析收藏纠错 + 选题

5. (2020九上·商河期末) 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果

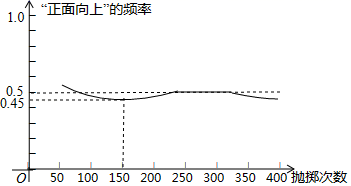
下面有三个推断：

①当抛掷次数是100时，计算机记录“正面向上”的次数是47，所以“正面向上”的概率是0.47；

②随着试验次数的增加，“正面向上”的频率总在0.5附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.5；

③若再次用计算机模拟此实验，则当抛掷次数为150时，“正面向上”的频率一定是0.45．

其中合理的是（　　）

A . ① B . ② C . ①② D . ①③

答案解析收藏纠错 + 选题
6. (2022八上·苍南月考) 从分别写有数字1，2，3，4，5的5张卡片中任意取出两张，把第一张卡片上的数字作为十位数字，第二张卡片上的数字作为个位数字，组成一个两位数，则所组成的数是3的倍数的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022八下·罗湖期末) 在一个不透明的布袋中，红色、黑色、白色的小球共有50个，除颜色外其他完全相同，乐乐通过多次摸球试验后发现，摸到红色球、黑色球的频率分别稳定在27%和43%，则口袋中白色球的个数很可能是（）

A . 15个 B . 20个 C . 25个 D . 30个

答案解析收藏纠错 + 选题
8. (2022七下·历下期末) 一个质量均匀的正方体骰子，六个面分别标有1，2，3，4，5，6，任意掷一次骰子，掷出结果为“2的倍数”的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题3分，共24分）

9. (2023九上·洪洞月考) 在一个不透明的盒子里装有黑、白两种颜色的球共50只，这些球除颜色外其余完全相同.小颖做摸球实验，搅匀后，她从盒子里随机摸出一只球记下颜色后，再把球放回盒子中.不断重复上述过程，下表是实验中的一组统计数据：

摸球的次数n	100	200	300	500	800	1 000	3 000
摸到白球的次数m	65	124	178	302	481	620	1845
摸到白球的频率 $\text{[math]}$	0.65	0.62	0.593	0.604	0.601	0.620	0.615

请估计：当n很大时，摸到白球的频率将会接近；（精确到0.1）

答案解析收藏纠错 + 选题

10. (2022八上·黄冈开学考) 为了估计鱼池里有多少条鱼，先捕上100条作上记号，然后放回到鱼池里，过一段时间，待有记号的鱼完全混合鱼群后，再捕上200条鱼，发现其中带记号的鱼有20条，则可判断鱼池里大约有条鱼．

答案解析收藏纠错 + 选题

11. (2022八下·泰兴期末) 某批排球的质量检验结果如下：

抽取的篮球数n	50	200	400	600	800	1000	1200
优等品的频数m	46	186	372	561	744	931	1116
优等品的频率 $\text{[math]}$	0.92	0.930	0.930	0.935	0.930	0.931	0.930

从这批排球中，任意抽取的一个排球是优等品的概率的估计值是．（精确到0.01）

答案解析收藏纠错 + 选题

12. (2021九下·厦门开学考) 在做“抛掷一枚质地均匀的硬币”试验时，下列说法正确的是.
①不同次数的试验，正面向上的频率可能会不相同

②当抛掷的次数 $\text{[math]}$ 很大时，正面向上的次数一定为 $\text{[math]}$

③多次重复试验中，正面向上发生的频率会在某个常数附近摆动，并趋于稳定

④连续抛掷 $\text{[math]}$ 次硬币都是正面向上，第 $\text{[math]}$ 次抛掷出现正面向上的概率小于 $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2022七下·宁阳期末) 长度分别为3cm，4cm，5cm，9cm的四条线段，任取其中三条能组成三角形的概率是．

答案解析收藏纠错 + 选题
14. (2022八下·桂平期末) 《论语十则》中有句话：“知之为知之不知为不知”这句话中“知”字出现的频率为．

答案解析收藏纠错 + 选题
15. (2022七下·长安期末) 如图，现有一个均匀的转盘被平均分成8等份，分别标有2、4、6、8、10、12、14、16这8个数字，转动转盘，当转盘停止时，指针指向的数字是3的倍数（当指针恰好指在分界线上时，重新转动转盘）的概率是．

答案解析收藏纠错 + 选题
16. (2022七下·长安期末) 如图，甲、乙、丙3人站在 $\text{[math]}$ 网格中的三个格子中，小王随机站在剩下的空格中，与图中3人均不在同一行的概率是．

答案解析收藏纠错 + 选题

三、解答题（共11题，共102分）

17. (2022七下·顺德期末) 现有四根长度为2cm、3cm、4cm、5cm的木棒，小明任意取一根木棒，能与长度为3cm、6cm的木棒拼成一个三角形木框的概率是多少？

答案解析收藏纠错 + 选题
18. (2019七下·三明期末) 如图所示，口袋中有5张完全相同的卡片，分别写有2cm，4cm，6cm，8cm和10cm，袋外有两张卡片，分别写有6cm和10cm，现随机从袋内取出一张卡片，与口袋外两张卡片放在一起，以卡片上的数量分别作为三条线段的长度，求这三条线段能构成等腰三角形的概率．

答案解析收藏纠错 + 选题
19. 小颖和小红两位同学在做投掷骰子（质地均匀的正方体）实验，他们共做了60次实验，实验的结果如下：
朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
（1）计算“3点朝上”的频率和“5点朝上”的频率．
（2）小颖说：“根据实验得出，出现5点朝上的机会最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次．”小颖和小红的说法正确吗？为什么？

答案解析收藏纠错 + 选题

20. (2022八上·郑州开学考) 数学试验

数学学习小组在学习“用频率估计概率”的数学活动课上，做投掷骰子（质地均匀的正方体）试验，他们共做了 $\text{[math]}$ 次试验，试验的结果如下：

向上点数	1	2	3	4	5	6
出现次数	12	19	15	18	20	$\text{[math]}$

（1）求表格中 $\text{[math]}$ 的值．
（2）计算“3点朝上”的频率．
（3）数学发现
数学学习小组针对数学试验的结果提出结论：“根据试验及 $\text{[math]}$ 用频率估计概率 $\text{[math]}$ 的知识，这次试验中出现1点朝上的概率是12%”你认为数学学习小组的结论正确吗？并说明理由．
（4）结论应用
在一个不透明的盒子里，装有40个黑球和若干个白球，它们除颜色外都相同，搅匀后从中任意摸出一个球，记下颜色再把它放回盒子中，不断重复试验，统计结果发现，随着试验次数越来越多，摸到黑球的频率逐渐稳定在0.2左右．据此估计盒子中大约有白球多少个？

答案解析收藏纠错 + 选题

21. (2022七下·泾阳期末) 某班在爱心义卖活动中设立了一个可以自由转动的转盘，如图所示，同时规定：顾客购物满50元就能获得一次转动转盘的机会，如表是活动中的统计数据：

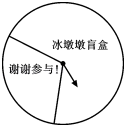
转动转盘的次数n	100	200	300	400	500
落在“谢谢参与！”区域的次数m	29	60	93	122	b
落在“谢谢参与！”区域的频率 $\text{[math]}$	0.29	0.3	0.31	a	0.29

（1）填空：a＝，b＝；
（2）若继续转动转盘，当n很大时，落在“谢谢参与！”区域的频率将会接近多少？若晓慧去转动该转盘一次，则她转到“谢谢参与！”的概率约是多少？（结果保留一位小数）

答案解析收藏纠错 + 选题

22. (2022八下·广陵期末) 在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个，某学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据：

摸球的次数n	1000	2000	3000	5000	8000	10000
摸到黑球的次数m	650	1180	1890	3100	4820	6013
摸到黑球的频率 $\text{[math]}$	0.65	0.59	0.63	0.62	0.6025	0.6013

（1）请估计：当n很大时，摸到黑球的频率将会接近（精确到0.1）；
（2）试估计袋子中有黑球个；
（3）若学习小组通过试验结果，想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%，则可以在袋子中增加相同的白球个或减少黑球个．

答案解析收藏纠错 + 选题

23. (2022七下·绥德期末) 某种油菜籽在相同条件下的发芽试验的结果如下：

试验的粒数n	20	80	100	200	400	800	1000	1500
发芽的粒数m	14	54	67	132	264	532	670	1000
发芽的频率 $\text{[math]}$	0.7	0.675	0.67	0.66	0.66	0.665	a	0.667

（1）填空：上表中a＝；
（2）根据上表，请估计，当n很大时，发芽的频率将会接近多少？（结果保留两位小数）
（3）根据上表，这种油菜籽发芽的概率的估计值是多少？（结果保留两位小数）

答案解析收藏纠错 + 选题

24. (2022七上·南宁期中) 为了做好校园新冠疫情防控工作，市教育局要求各学校每天抽取部分学生进行核酸检测.某天我校七年级各班做核酸检测人数（单位：人）分别为：23，31，27，36，30，15，24，25，28，29.
1. （1）每班做核酸检测人数以25人为标准，问七年级抽取人数总计超过多少人或不足多少人？
2. （2）按市教育局规定，当天七年级做核酸检测人数要超过年级总人数的40%，已知我校七年级学生共有650人，请你通过计算，判断七年级当天做核酸检测人数是否符合市教育局的要求？
答案解析收藏纠错 + 选题
25.
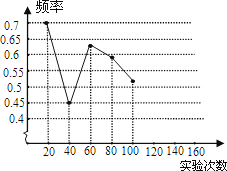
一粒木质中国象棋棋子“車”，它的正面雕刻一个“車”字，它的反面是平的，将棋子从一定高度下抛，落地反弹后可能是“車”字面朝上，也可能是“車”字朝下．由于棋子的两面不均匀，为了估计“車”字朝上的机会，某实验小组做了棋子下抛实验，并把实验数据整理如下：
实验次数
20
40
60
80
100
120
140
160
“車”字朝上的频数
14
18
38
47
52

78
88
相应的频率
0.7
0.45
0.63
0.59
0.52
0.55
0.56

（1）请将表中数据补充完整，并画出折线统计图中剩余部分．
（2）如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的机会，请估计这个机会约是多少？
（3）在（2）的基础上，进一步估计：将该“車”字棋子，按照实验要求连续抛2次，则刚好使“車”字一次字面朝上，一次朝下的可能性为多少？

答案解析收藏纠错 + 选题
26. (2022八上·沙坪坝开学考) “无体育不南开”，我校为了了解初中学生在暑假期间每周的运动时间（单位为小时，简记为h），随机抽取了部分初中学生进行调查，根据调查结果，绘制成如下不完整的统计图表．
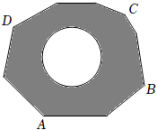
请根据相关信息，解答下列问题：
1. （1）本次调查的总人数为，扇形统计图中的m＝；
2. （2）把条形统计图补充完整；
3. （3）若从被调查的学生中随机抽取一人，这名学生每周运动时间不足8小时的概率是多少？
答案解析收藏纠错 + 选题

27. (2022八上·河南开学考) 如图，地面上有一个不规则的封闭图形ABCD，为求得它的面积，小明设计了一个如下方法：

①在此封闭图形内画出一个半径为1米的圆．

②在此封闭图形旁边闭上眼晴向封闭图形内掷小石子（可把小石子近似地看成点），记录如下：

掷小石子落在不规则图形内的总次数	50	150	300	500	…
小石子落在圆内（含圆上）的次数m	20	59	123	203	…
小石子落在圆外的阴影部分（含外缘）的次数n	29	91	176	293	…
m∶n	0.689	0.694	0.689	0.706