陕西省延安市2023年中考数学第一次模拟考试卷

更新时间：2024-07-13 浏览次数：109 类型：中考模拟

一、单选题

1. (2023·雁塔模拟) 2.5的相反数是（）

A . 2.5 B . -2.5 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·汉中模拟) 如图，将木条a，b与c钉在一起，∠1＝85°，∠2＝45°，要使木条a与b平行，木条a按箭头方向旋转的度数至少是（）

A . 15° B . 25° C . 35° D . 40°

答案解析收藏纠错 + 选题
3. (2023九上·西安开学考) 计算： $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·雁塔模拟) 如图，四边形ABCD的对角线互相平分，要使它成为矩形，那么需要添加的条件是（）

A . AB=BC B . AC垂直BD C . ∠A=∠C D . AC=BD

答案解析收藏纠错 + 选题
5. (2023八上·泗县月考) 已知二元一次方程组 $\text{[math]}$ 的解为 $\text{[math]}$ ，则在同一平面直角坐标系中，直线 $\text{[math]}$ ： $\text{[math]}$ 与直线 $\text{[math]}$ ： $\text{[math]}$ 的交点坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九上·惠东期末) 如图， $\text{[math]}$ 内接于⊙ $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023·延安模拟) 如图是四个二次函数的图象，则a、b、c、d的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

8. (2024九下·陇县模拟) $\text{[math]}$ 的大小顺序是（用“>”号连接）.

答案解析收藏纠错 + 选题
9. (2023·汉中模拟) 计算 $\text{[math]}$ 的结果是.

答案解析收藏纠错 + 选题
10. (2023·延安模拟) 比较大小： $\text{[math]}$ 0.（填“ $\text{[math]}$ ”、“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）

答案解析收藏纠错 + 选题
11. (2023·延安模拟) 数学中，把 $\text{[math]}$ 这个比例称为黄金分割比.鹦鹉螺曲线的每个半径和后一个半径的比都是黄金比例，是自然界最美的鬼斧神工.如图， $\text{[math]}$ 是 $\text{[math]}$ 的黄金分割点 $\text{[math]}$ ，若线段 $\text{[math]}$ 的长为 $\text{[math]}$ ，则 $\text{[math]}$ 的长为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. 已知点A(−2，m)在一个反比例函数的图象上，点A′与点A关于y轴对称.若点A′在正比例函数 $\text{[math]}$ 的图象上，则这个反比例函数的表达式为.

答案解析收藏纠错 + 选题
13. (2023·未央模拟) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为线段 $\text{[math]}$ 的中点，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 的方向在 $\text{[math]}$ 和 $\text{[math]}$ 上运动，将矩形沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 的对应点为 $\text{[math]}$ ，当点 $\text{[math]}$ 恰好落在矩形的对角线上时，点 $\text{[math]}$ 运动的距离为.

答案解析收藏纠错 + 选题

三、解答题

14. (2023·渭南模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2023·未央模拟) 解不等式组 $\text{[math]}$ 并写出该不等式组的最小整数解．

答案解析收藏纠错 + 选题
16. (2023·渭南模拟) 化简： $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2023·商洛模拟) 已知点 $\text{[math]}$ 是平面直角坐标系中的点.
1. （1）若点A在第二象限的角平分线上，求a的值；
2. （2）若点A在第三象限，且到两坐标轴的距离和为9，请确定点A的坐标.
答案解析收藏纠错 + 选题
18. (2023·洮北模拟) 如图，在Rt△ABC中，∠B＝90°，CD∥AB，DE⊥AC于点E，且CE＝AB．求证：△CED≌△ABC．

答案解析收藏纠错 + 选题
19. (2023·安康模拟) 如图，在平面直角坐标系中， $\text{[math]}$ 的顶点坐标分别为 $\text{[math]}$ .在图中作出 $\text{[math]}$ 关于y轴对称的 $\text{[math]}$ ，并写出点B、C的对应点 $\text{[math]}$ 、 $\text{[math]}$ 的坐标.

答案解析收藏纠错 + 选题
20. (2023·汉中模拟) 保护环境，人人有责，某校为培养学生“垃圾分类，从我做起”的环保意识，组织开展“游戏互动”､“趣味问答”､“模拟投放”三项活动（分别以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 来依次表示这三项活动）.活动开始前，将 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 这三个字母分别写在三张无差别不透明的卡片正面上，洗匀后正面向下放在桌面上，小南同学先从中随机抽取一张卡片放回后洗匀，小晶同学从中再随机抽取一张卡片.
1. （1）求小南抽到参加“趣味问答”活动的概率；
2. （2）用列表法或画树状图法，求小南和小晶都抽到参加“趣味问答”活动的概率.
答案解析收藏纠错 + 选题
21. (2023·汉中模拟) 已知有一块三角形材料 $\text{[math]}$ ，其中 $\text{[math]}$ ，高 $\text{[math]}$ ，现需要在三角形 $\text{[math]}$ 上裁下一个正方形材料做零件，使得正方形 $\text{[math]}$ 的顶点 $\text{[math]}$ 、 $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ 上， $\text{[math]}$ 、 $\text{[math]}$ 在 $\text{[math]}$ 上，裁下的正方形 $\text{[math]}$ 的边长是多少？

答案解析收藏纠错 + 选题
22. (2023·柯桥模拟) 如图1，小明家、食堂、图书馆在同一条直线上，小明从食堂吃完早餐，接着骑自行车去图书馆读书，然后以相同的速度原路返回家.如图2中反映了小明离家的距离 $\text{[math]}$ 与他所用时间 $\text{[math]}$ 之间的函数关系.
1. （1）小明家与图书馆的距离为 $\text{[math]}$ ，小明骑自行车速度为 $\text{[math]}$ ；
2. （2）求小明从图书馆返回家的过程中， $\text{[math]}$ 与 $\text{[math]}$ 的函数解析式；
3. （3）当小明离家的距离为 $\text{[math]}$ 时，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
23. (2023·汉中模拟) 为迎接党的二十大胜利召开，某校开展了以“不忘初心跟党走”为主题的读书活动，学校对本校学生9月份“读书量”进行了随机抽样调查，对所有随机抽取的数据进行了统计，并绘制成如下两幅不完整的统计图.
1. （1）求出此次抽样调查的学生总数，并补全条形统计图；
2. （2）本次所抽取学生9月份“读书量”的众数为本；
3. （3）根据抽样调查的结果，请你估计该校1000名学生中，9月份“读书量”不少于4本的学生人数.
答案解析收藏纠错 + 选题
24. (2023·宝鸡模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的角平分线.
1. （1）如图1，点E、F分别是线段 $\text{[math]}$ 、 $\text{[math]}$ 上的点，且 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的延长线交于点G，则 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是，位置关系是；
2. （2）如图2，点E、F分别在 $\text{[math]}$ 和 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ， $\text{[math]}$ 的延长线交 $\text{[math]}$ 于点G.
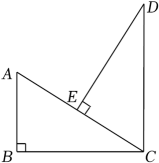
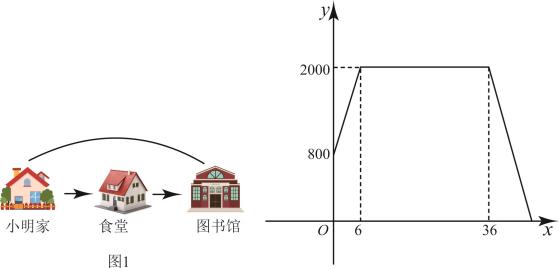
  ①（1）中的结论还成立吗？如果成立，请给出证明；如果不成立，请说明理由；
  ②连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
25. (2023·延安模拟) 卡塔尔世界杯完美落幕.在一场比赛中，球员甲在离对方球门30米处的 $\text{[math]}$ 点起脚吊射（把球高高地挑过守门员的头顶，射入球门），假如球飞行的路线是一条抛物线，在离球门14米时，足球达到最大高度8米.如图所示，以球员甲所在位置 $\text{[math]}$ 点为原点，球员甲与对方球门所在直线为 $\text{[math]}$ 轴，建立平面直角坐标系.
1. （1）求满足条件的抛物线的函数表达式；
2. （2）如果葡萄牙球员 $\text{[math]}$ 罗站在球员甲前3米处， $\text{[math]}$ 罗跳起后最高能达到2.88米，那么 $\text{[math]}$ 罗能否在空中截住这次吊射？
答案解析收藏纠错 + 选题
26. (2023·安康模拟) 如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为倍角三角形，并称这两个角的公共边为底边.

例如：若△ABC中，∠A＝2∠B，则△ABC为以边AB为底边的倍角三角形.
1. （1）已知△ABC为倍角三角形，且 $\text{[math]}$ .
  ①如图1，若BD为△ABC的角平分线，则图中相等的线段有，图中相似三角形有；
  ②如图2，若AC的中垂线交边BC于点E，连接AE，则图中等腰三角形有.
2. （2）【问题解决】
  如图3，现有一块梯形板材ABCD， $\text{[math]}$ ， ∠A＝90°，AB＝48，BC＝132，AD＝68.工人师傅想用这块板材裁出一个△BCP型部件，使得点P在梯形ABCD的边上，且△BCP为以BC为底边的倍角三角形.工人师傅在这块板材上的作法如下：
  ①作BC的中垂线l交BC于点E；
  
  ②在BC上方的直线l上截取EF＝33，连接CF并延长，交AD于点P；
  
  ③连接BP，得△BCP.
  
  1）请问，若按上述作法，裁得的△BCP型部件是否符合要求？请证明你的想法.
  
  2）是否存在其它满足要求的△BCP？若存在，请画出图形并求出CP的长；若不存在，请说明理由.
答案解析收藏纠错 + 选题