2023学年沪科版数学七年级下册期中考试质量检测卷（一）

更新时间：2023-03-30 浏览次数：100 类型：期中考试

一、单选题（每题4分，共40分）

1. (2023八上·东方期末) 下列各数中，是无理数的为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·翼城模拟) 原子是化学变化中的最小微粒，按照国际单位制的规定，质量单位是“kg”．例如：1个氧原子的质量是 $\text{[math]}$ ．如果小数0.000…02657用科学记数法表示为 $\text{[math]}$ ，那么这个小数中的“0”有（）

A . 25个 B . 26个 C . 27个 D . 28个

答案解析收藏纠错 + 选题
3. (2023·汨罗模拟) 下列运算结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八上·蒲城期末) 已知 $\text{[math]}$ ， a介于两个连续自然数之间，则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八上·凤凰期末) 下列各式从左到右的变形中，是因式分解且完全正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022八上·新昌月考) 某商畈去菜摊买黄瓜，他上午买了30千克，价格为每千克x元，下午，他又买了20千克，价格为每千克y元﹒后来他以每千克 $\text{[math]}$ 元的价格卖完后，结果发现自己赔了钱，其原因是（）

A . $\text{[math]}$ ＜y B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·牡丹江模拟) 某种商品每件的进价为120元，商场按进价提高 $\text{[math]}$ 标价，为增加销量，准备打折销售，但要保证利润率不低于 $\text{[math]}$ ，则至多可以打（）折

A . 7 B . 7.5 C . 8 D . 8.5

答案解析收藏纠错 + 选题
8. (2022·邵阳) 关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 有且只有三个整数解，则 $\text{[math]}$ 的最大值是（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
9. (2023九下·柳州月考) 如图，两个正方形边长分别为a，b，已知 $\text{[math]}$ ， $\text{[math]}$ ，则阴影部分的面积为（）

A . 10 B . 11 C . 12 D . 13

答案解析收藏纠错 + 选题
10. (2021七下·泗县期末) 根据等式： $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ……的规律，则可以推算得出 $\text{[math]}$ 的末位数字是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每空4分，共20分）

11. (2023·青羊模拟) 比较大小： $\text{[math]}$ $\text{[math]}$ .（填“>”，“<”，或“＝”）

答案解析收藏纠错 + 选题
12. (2021七下·南开期中) 已知 $\text{[math]}$ ＝1.449， $\text{[math]}$ ＝4.573，则 $\text{[math]}$ 是．

答案解析收藏纠错 + 选题
13. (2023八上·安顺期末) 若 $\text{[math]}$ 是关于 $\text{[math]}$ 的完全平方式，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2021七下·萧山期末) 两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为 $\text{[math]}$ ；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为 $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ ＋ $\text{[math]}$ ＝；当 $\text{[math]}$ ＋ $\text{[math]}$ ＝40时，则图3中阴影部分的面积 $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题（共9题，共90分）

15. (2023九下·柳州月考) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2022八下·紫金期末) 解不等式组： $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2023八上·西安期末) 已知： $\text{[math]}$ 的立方根是 $\text{[math]}$ ， c是 $\text{[math]}$ 的整数部分.
1. （1）求a，b，c的值；
2. （2）求 $\text{[math]}$ 的平方根.
答案解析收藏纠错 + 选题
18. (2021七下·兰山期末) 一艘轮船从某江上游的 $\text{[math]}$ 地匀速驶到下游的 $\text{[math]}$ 地用了 $\text{[math]}$ ，从 $\text{[math]}$ 地匀速返回 $\text{[math]}$ 地用了不到12h，这段江水的流速为 $\text{[math]}$ ，轮船在静水中的往返速度不变，且为正整数．试求轮船在静水中速度的最小值是多少？

答案解析收藏纠错 + 选题
19. (2022七下·邗江期末) 小明和小红在计算 $\text{[math]}$ 时，分别采用了不同的解法.
小明的解法： $\text{[math]}$ ，
小红的解法： $\text{[math]}$ .
请你借鉴小明和小红的解题思路，解决下列问题：
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）已知 $\text{[math]}$ 满足 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
20. (2022七下·长兴期末) [学习材料]——拆项添项法
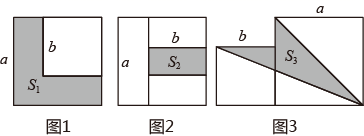
在对某些多项式进行因式分解时，需要把多项式中的某一项拆成两项或多项，或者在多项式中添上两个仅符号相反的项，这样的分解因式的方法称为拆项添项法．如：

例1：分解因式：x²+2x-3．

解：原式=x²+2x+1-1-3=（x+1）²-4=（x+1-2）（x+1+2）=（x-1）（x+3）．

例2：分解因式：x³+5x-6．

解：原式=x³-x+6x-6=x（x²-1）+6（x-1）=（x-1）（x²+x+6）．

[知识应用]请根据以上材料中的方法，解决下列问题：
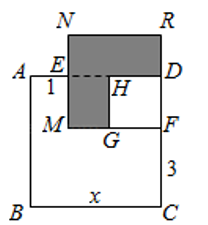
1. （1）分解因式：x²+14x-51=．
2. （2）化简： $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2023八上·安岳期末) 若 $\text{[math]}$ 满足 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
解：设 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）若 $\text{[math]}$ 满足 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）
  【拓展应用】
  如图，已知正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ 分别是 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，长方形 $\text{[math]}$ 的面积是 $\text{[math]}$ ，分别以 $\text{[math]}$ 为边作正方形 $\text{[math]}$ .
  ① $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ；(用含 $\text{[math]}$ 的式子表示)
  
  ②求阴影部分的面积.
答案解析收藏纠错 + 选题
22. (2023·湘潭模拟) 随着新能源汽车的发展，某公交公司将用新能源汽车淘汰某一条线路上“冒黑烟”较严重的燃油公交车，计划购买A型和B型新能源公交车共10辆.若购买A型公交车1辆和B型公交车2辆共需300万元；且购买一辆A型公交车的费用比购买一辆B型公交车的费用少30万元.
1. （1）求A型和B型公交车的单价分别为多少万元？
2. （2）预计在该条线路上A型和B型公交车每辆日均载客量为160人次和200人次，若该公司购买A型和B型公交车的总费用不超过1000万元，且确保这10辆公交车在该线路的日均载客量总和不少于1800人次，则该公司有哪几种购车方案？哪种购车方案的总费用最少？最少总费用是多少？
答案解析收藏纠错 + 选题
23. (2022八上·岳麓开学考) 若不等式 $\text{[math]}$ 组 $\text{[math]}$ 只有 $\text{[math]}$ 个正整数解 $\text{[math]}$ 为自然数 $\text{[math]}$ ，则称这个不等式 $\text{[math]}$ 组 $\text{[math]}$ 为 $\text{[math]}$ 阶不等式 $\text{[math]}$ 组 $\text{[math]}$ ．
我们规定：当 $\text{[math]}$ 时，这个不等式 $\text{[math]}$ 组 $\text{[math]}$ 为 $\text{[math]}$ 阶不等式 $\text{[math]}$ 组 $\text{[math]}$ ．

例如：不等式 $\text{[math]}$ 只有4个正整数解，因此称其为4阶不等式．

不等式组 $\text{[math]}$ 只有3个正整数解，因此称其为3阶不等式组．

请根据定义完成下列问题：
1. （1） $\text{[math]}$ 是阶不等式； $\text{[math]}$ 是阶不等式组；
2. （2）若关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 是4阶不等式组，求 $\text{[math]}$ 的取值范围；
3. （3）关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 的正整数解有 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 其中 $\text{[math]}$
  如果 $\text{[math]}$ 是 $\text{[math]}$ 阶不等式组，且关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的解是 $\text{[math]}$ 的正整数解 $\text{[math]}$ ，请求出 $\text{[math]}$ 的值以及 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题