2023年浙教版数学七年级下学期高分速效复习6 整式的乘除（...

更新时间：2023-04-04 浏览次数：52 类型：复习试卷

一、单选题（每题2分，共20分）

1. (2022七下·包河期中) 已知 $\text{[math]}$ ，则x、y、z三者之间关系正确的是（）

A . xy=2z B . x+y=2z C . x+2y=2z D . x+2y=z

答案解析收藏纠错 + 选题
2. (2023八上·北塔月考) 下列计算中，错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023八上·翠屏月考) 已知单项式6a^m+1bⁿ⁺¹与﹣4a^2m^﹣1b²ⁿ^﹣1的积与7a³b⁶是同类项，则mⁿ的值为（　　）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
4. (2022八上·宝安期末) 若多项式 $\text{[math]}$ 能分解成两个一次因式的积，且其中一个次因式 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 1 B . 5 C . -1 D . -5

答案解析收藏纠错 + 选题
5. (2022七下·鄞州期末) 有两个正方形A，B.现将B放在A的内部得图甲，将A，B构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12，若三个正方形A和两个正方形B得图丙，则阴影部分的面积为（　　）

A . 28 B . 29 C . 30 D . 31

答案解析收藏纠错 + 选题
6. (2019八上·同安月考) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为 $\text{[math]}$ ）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
7. (2020七下·西湖期末) 已知2ⁿ＋2¹²＋1（n＜0）是一个有理数的平方，则n的值为（）

A . ﹣16 B . ﹣14 C . ﹣12 D . ﹣10

答案解析收藏纠错 + 选题
8. (2023·翼城模拟) 原子是化学变化中的最小微粒，按照国际单位制的规定，质量单位是“kg”．例如：1个氧原子的质量是 $\text{[math]}$ ．如果小数0.000…02657用科学记数法表示为 $\text{[math]}$ ，那么这个小数中的“0”有（）

A . 25个 B . 26个 C . 27个 D . 28个

答案解析收藏纠错 + 选题
9. (2022七下·馆陶期末) 已知 $\text{[math]}$ ，给出四个代数式，其中有一个代数式与其余代数式的化简结果不相等，则这个代数式是（）

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题
10. (2023八上·江安期中) 我们经常利用完全平方公式以及变形公式进行代数式变形.已知关于a的代数式 $\text{[math]}$ ，请结合你所学知识，判断下列说法：①当 $\text{[math]}$ 时， $\text{[math]}$ ；②无论a取任何实数，不等式 $\text{[math]}$ 恒成立；③若 $\text{[math]}$ ，则 $\text{[math]}$ .正确的有（）

A . 3个 B . 2个 C . 1个 D . 0个

答案解析收藏纠错 + 选题

二、填空题（每空3分，共18分）

11. (2023九下·沭阳月考) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2019八上·唐河期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2022七下·渠县月考) 某同学在计算多项式A乘 $\text{[math]}$ 时，因抄错运算符号，算成了加 $\text{[math]}$ ，得到的结果是 $\text{[math]}$ ，那么正确的计算结果是.

答案解析收藏纠错 + 选题
14. (2022八上·科尔沁期末) $\text{[math]}$ 的结果是．

答案解析收藏纠错 + 选题
15. (2022七下·泗县期中) 已知（2021-a）（a-2022）＝5，则（a-2021）²+（a-2022）²＝．

答案解析收藏纠错 + 选题
16. (2020七下·黄岛期中) 如图，现有A，C两类正方形卡片和B类长方形卡片各若干张，用它们可以拼成一些新的长方形．如果要拼成一个长为（3a+b），宽为（a+2b）的长方形，那么需要B类长方形卡片张．

答案解析收藏纠错 + 选题

三、计算题（共3题，共27分）

17. (2022七下·成都月考) 计算题
1. （1） $\text{[math]}$ ；
2. （2） 2021²-4040×2021+2020²；
3. （3） 99×101；
4. （4）（1 $\text{[math]}$ ）（1 $\text{[math]}$ ）（1 $\text{[math]}$ ）（1 $\text{[math]}$ ）…（1 $\text{[math]}$ ）.
答案解析收藏纠错 + 选题
18. (2022八上·乐山期中) 化简求值：
1. （1） $\text{[math]}$ 其中 $\text{[math]}$ ；
2. （2） $\text{[math]}$ 其中 $\text{[math]}$ .
答案解析收藏纠错 + 选题
19. 先化简，再求值.
1. （1） $\text{[math]}$ ，其中 $\text{[math]}$ ；
2. （2）已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值；
3. （3）已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题

四、解答题（共2题，共14分）

20. 若 $\text{[math]}$ 且 $\text{[math]}$ 是正整数)，则 $\text{[math]}$ .利用上面的结论解决下面的问题.
1. （1）如果 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）如果 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
21. (2021八上·崆峒期末) 某种产品的原料提价，因而厂家决定对产品进行提价，现有三种方案：
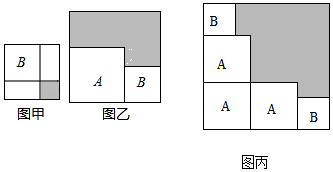
①第一次提价p%，第二次提价q%；

②第一次提价q%，第二次提价p%；

③第一、二次提价均为 $\text{[math]}$ .

其中p，q是不相等的正数，三种方案哪种提价最多？

答案解析收藏纠错 + 选题

五、解答题（共5题，共41分）

22. (2023八上·内江期末) 我们将 $\text{[math]}$ 进行变形，如： $\text{[math]}$ ， $\text{[math]}$ 等.根据以上变形解决下列问题：
1. （1）已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ；
2. （2）若x满足 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
3. （3）如图，在长方形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点E、F分别是 $\text{[math]}$ 、 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，分别以 $\text{[math]}$ 、 $\text{[math]}$ 为边在长方形 $\text{[math]}$ 外侧作正方形 $\text{[math]}$ 和 $\text{[math]}$ ，若长方形 $\text{[math]}$ 的面积为40，求图中阴影部分的面积和.
答案解析收藏纠错 + 选题
23. (2022八上·丰城期中) 阅读材料后解决问题：
小明遇到下面一个问题：
计算（2+1）（2²+1）（2⁴+1）（2⁸+1）．
经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：（2+1）（2²+1）（2⁴+1）（2⁸+1）
=（2+1）（2﹣1）（2²+1）（2⁴+1）（2⁸+1）
=（2²﹣1）（2²+1）（2⁴+1）（2⁸+1）
=（2⁴﹣1）（2⁴+1）（2⁸+1）
=（2⁸﹣1）（2⁸+1）
=2¹⁶﹣1
请你根据小明解决问题的方法，试着解决以下的问题：
1. （1）（2+1）（2²+1）（2⁴+1）（2⁸+1）（2¹⁶+1）=．
2. （2）（3+1）（3²+1）（3⁴+1）（3⁸+1）（3¹⁶+1）=．
3. （3）化简：（m+n）（m²+n²）（m⁴+n⁴）（m⁸+n⁸）（m¹⁶+n¹⁶）．
答案解析收藏纠错 + 选题
24. (2022八上·乐清开学考) 数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片是边长为a的正方形，B种纸片是边长为b的正方形，C种纸片是长为b，宽为a的长方形.并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形.
1. （1）请用两种不同的方法求图2大正方形的面积：
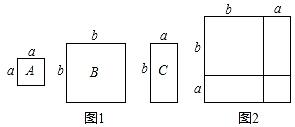
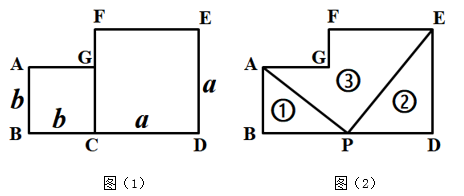
  方法1：；方法2：；
2. （2）观察图2，请你写出代数式：（a+b）² ， a²+b² ， ab之间的等量关系；
3. （3）根据（2）题中的等量关系，解决如下问题：
  ①已知：a+b＝5，（a﹣b）²＝13，求ab的值；
  ②已知（2021﹣a）²+（a﹣2020）²＝5，求（2021﹣a）（a﹣2020）的值.
答案解析收藏纠错 + 选题
25. (2021七下·上虞期末) 在学了乘法公式“(a±b)²= a²±2ab+b²”的应用后，王老师提出问题：求代数式x²＋4x＋5的最小值.要求同学们运用所学知识进行解答.
同学们经过探索、交流和讨论，最后总结出如下解答方法：

解：x²＋4x＋5=x²＋4x+2²-2²+5=(x+2)²+1，

∵(x+2)²≥0，".(x+2)²+1≥1.

当(x+2)²=0时，(x+2)²+1的值最小，最小值是1

∴x²+4x＋5的最小值是1.

请你根据上述方法，解答下列各题：
1. （1）直接写出(x-1)²+3的最小值为
2. （2）求代数式x²＋10x＋32的最小值.
3. （3）若7x-x²+y-11=0，求x＋y的最小值.
答案解析收藏纠错 + 选题
26. (2022七下·杭州期中) 两个边长分别为a、b（a>b）的正方形如图（1）放置，现在取BD的中点P，连接PA、PE，如图（2），把图形分割成三部分，分别标记①、②、③，对应的图形面积分别记为S_①、S_②、S_③.
1. （1）用字母a、b分别表示S_①、S_②.
2. （2）若a-b=2，ab=15，求S_①+S_②.
3. （3）若S_①+S_②=3，ab=1，求S_③.
答案解析收藏纠错 + 选题