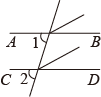
 B .
B . 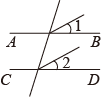 C .
C . 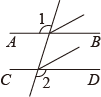 D .
D . 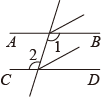
| 证明:如图,∵ ∵ ∴∠1=∠2,∴
|
已知该证明过程是正确的,则证明的真命题是( )

已知:的三个内角为
、
、
求证: .
证法1:如图 ∵ ∵ ∴ |
|
证法2:如图,延长 ∴
∵ ∴ 即 |
|
下列说法正确的是( )
证法1:如图, ∵∠A=70°,∠B=63°, 且∠ACD=133°(量角器测量所得) 又∵133°=70°+63°(计算所得) ∴∠ACD=∠A+∠B(等量代换). | 证法2:如图, ∵∠A+∠B+∠ACB=180°(三角形内角和定理), 又∵∠ACD+∠ACB=180°(平角定义), ∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换). ∴∠ACD=∠A+∠B(等式性质). |
下列说法正确的是( )

如图、与
互补,
, 求证:
.对于本题小丽是这样证明的,请你将她的证明过程补充完整.
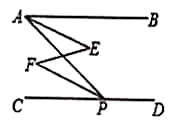
证明:与
互补,(已知)
.( )
.( )
, (已知)
, (等量代换)
即_▲_=_▲_.
.( )
.( )

请完善证明过程,并在括号内填上相应依据:
证明:
∵ , ( )
∴ ▲ ▲ , ( )
∴ , ( )
∴ , ( )
∵(已知),
∴ ▲ ▲ , ( )
∴平分
.( )

请将下面的证明过程补充完整:
证明:∵(已知),
∴ , (① )
∵平分
,
∴②▲ .(③ )
∴.(④ )
∵(已知),
∴⑤▲ .(⑥ )
∴.(⑦ )
∴.(⑧ )
如图, ,
平分
,
平分
,
. 求证:
.

证明:∵平分
,
平分
, (已知)
∴ ▲ ,
▲ . (角平分线的定义)
又∵ , (已知)
∴∠ ▲ =∠ ▲ . (等量代换)
又∵ , (已知)
∴∠ ▲ ∠ ▲ . (等量代换)
∴ . ( )
已知:如图, 求证: | |
方法一 证明:如图,过点A作
| 方法二 证明:如图,过点C作 |