【概念提出】若对x只加上(减去)一个常数,则该函数为一级函数:对x只乘(除以)一个常数(不为1),则该函数为二级函数:对x只进行乘方(开方)运算,则该函数为三级函数;若对某级函数中自变量的代数式再进行不同的运算,则新函数为该级函数的衍生函数.
①是二级函数;
②将再进行减法运算,所得衍生函数的图象与原图象平行;
③将再除以2所得衍生函数的图象是把函数
的图象上各点的横坐标不变,纵坐标变为原来的
倍;
④将先减3再平方与先平方再减3所得衍生函数是同一个函数.

①已知直线y=x+3与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;
②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A,C分别在坐标轴上,P是线段BC上动点,已知点D在第一象限,且是直线y=2x-5上的一点,若△APD是不以A为直角顶点的等腰直角三角形,请直接写出所有符合条件的点D的坐标.
①直接写出该函数与y轴的交点坐标;
②若直线y=4x+t与该函数只有一个交点,求t的取值范围;
例如、
、
都是“不动点”,已知双曲线
①当时,求
的取值范围.
②如果 , 过双曲线
图象上第一象限的“不动点”作平行于
轴的直线
, 若抛物线上有四个点到
的距离为
, 直接写出
的取值范围.
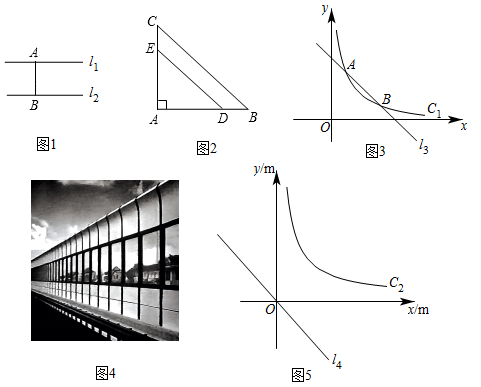
例如,如图1, , 线段
的长度称为点A与直线
之间的距离,当
时,线段
的长度也是
与
之间的距离.
解:∵ , ∴
.
∵ , ∴
.
若函数 , 求y的取值范围.