北师大版数学九年级上册同步练习——第二章《一元二次方程》6 ...

更新时间：2023-07-17 浏览次数：89 类型：同步测试

一、选择题

1. (2023八下·温州期中) 如图，某景区内有一块长方形油菜花田地（单位：m），现在其中修建观花道（阴影部分）供游人赏花，要求观花道面积是30．设观花道的直角边为x，则可列方程为（）

A . （10+x）（9+x）＝30 B . （10+x）（9+x）＝60 C . （10-x）（9-x）＝30 D . （10-x）（9-x）＝60

答案解析收藏纠错 + 选题
2. (2023·西山模拟) 为加快推动城市生态建设的步伐，形成“城在林中、园在城中、山水相依，林路相随”的生态格局，昆明市政府计划在某公园的一块矩形空地上修建草坪，如图，矩形长为 $\text{[math]}$ ，宽为 $\text{[math]}$ ，在矩形内的四周修筑同样宽的道路，余下的铺上草坪．要使草坪的面积为 $\text{[math]}$ ，道路的宽度应为多少？设矩形地块四周道路的宽度为 $\text{[math]}$ ，根据题意，下列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·济南期末) 某超市一月份的营业额为300万元，第一季度的营业额共1200万元，如果平均每月增长率为 $\text{[math]}$ ，则由题意可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·城厢月考) 根据福建省统计局数据，福建省2020年的地区生产总值为43903.89亿元，2022年的地区生产总值为53109.85亿元．设这两年福建省地区生产总值的年平均增长率为x，根据题意可列方程（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八上·绍兴月考) 如图，某小区规划在一个长 $\text{[math]}$ 、宽 $\text{[math]}$ 的长方形场地 $\text{[math]}$ 上修建三条同样宽的通道，使其中两条与 $\text{[math]}$ 平行，另一条与 $\text{[math]}$ 平行，其余部分种花草．要使每一块草坪的面积都为 $\text{[math]}$ ，那么通道的宽 $\text{[math]}$ 应该满足的方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八下·萧山期中) 如图，面积为 $\text{[math]}$ 的长方形试验田一面靠墙 $\text{[math]}$ 墙的长度不限 $\text{[math]}$ ，另外三面用 $\text{[math]}$ 长的篱笆围成，平行于墙的一边开有一扇 $\text{[math]}$ 宽的门 $\text{[math]}$ 门的材料另计 $\text{[math]}$ 设试验田垂直于墙的一边 $\text{[math]}$ 的长为 $\text{[math]}$ ，则所列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·大方模拟) 春意复苏，郑州绿化工程正在如火如荼地进行着，某工程队计划将一块长64m，宽40m的矩形场地建设成绿化广场如图，广场内部修建三条宽相等的小路，其余区域进行绿化．若使绿化区域的面积为广场总面积的80%，求小路的宽，设小路的宽为x m，则可列方程（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

8. (2024九下·大足期末) 某校截止到 $\text{[math]}$ 年底，校园绿化面积为 $\text{[math]}$ 平方米．为美化环境，该校计划 $\text{[math]}$ 年底绿化面积达到 $\text{[math]}$ 平方米．利用方程想想，设这两年绿化面积的年平均增长率为 $\text{[math]}$ ，则依题意列方程为．

答案解析收藏纠错 + 选题
9. (2024九上·重庆市开学考) 为了加快数字化城市建设，某市计划新建一批智能充电桩，第一个月新建了301个充电桩，第三个月新建了500个充电桩，设该市新建智能充电桩个数的月平均增长率为 $\text{[math]}$ ，根据题意，请列出方程．

答案解析收藏纠错 + 选题
10. (2023·陇县模拟) 《田亩比类乘除捷法》是我国古代数学家杨辉的著作，其中有一个数学问题：“直田积八百九十一步，只云长阔共六十步，问长多阔几何”．意思是：一块矩形田地的面积为891平方步，只知道它的长与宽共60步，问它的长比宽多多少步？根据题意得，长比宽多步．

答案解析收藏纠错 + 选题
11. (2024九上·南宁开学考) 如图，用一面足够长的墙为一边，其余三边用总长34米的围栏建两个面积相同的生态园，两个生态园各留一扇宽为1米的门．由于场地限制，垂直于墙的一边长不超过6米（围栏宽忽略不计）．每个生态园的面积为48平方米，则每个生态园垂直于墙的一边长为．

答案解析收藏纠错 + 选题
12. (2023七下·顺义期中) 有一个正方形的花园，如果它的边长增加 $\text{[math]}$ ，那么花园面积将增加 $\text{[math]}$ ，则原花园的面积为．

答案解析收藏纠错 + 选题

三、解答题

13. (2023·武功模拟) 如图，某小区矩形绿地的长宽分别为30m，20m．现计划对其进行扩充，将绿地的长、宽增加相同的长度后，得到一个新的矩形绿地．若扩充后的矩形绿地面积为 $\text{[math]}$ ，求新的矩形绿地的长与宽．

答案解析收藏纠错 + 选题

14. (2023八下·温州期中) 根据以下信息，探索完成任务．

如何设计种植方案？

素材1

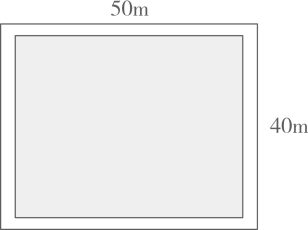
小明以“种植农作物”为主题在自己家100平方米的土地上进行课外实践，现有A、B两种作物的相关信息如下表所示：

	A作物	B作物
每平方米种植株树(株)	2	10
单株产量(千克)	1.2	0.5

素材2

由于A作物植株间距较大，可增加A作物每平方米的种植株树．经过调研发现，每平方米种植A作物每增加1株，A作物的单株产量减少0.1千克．

素材3

若同时种植A、B两种作物，实行分区域种植．

问题解决

单一种植(全部种植A作物)

任务1：明确数量关系

设每平方米增加x株A作物(x 为正整数)，则每平方米有 ▲ 株，单株产量为 ▲ 千克．(用含x的代数式表示)

任务2：计算产量

要使A作物每平方米产量为4.8千克，则每平方米应种植多少株？

单一种植(全部种植A作物)

任务3：规划种植方案

设这100平方米的土地中有a平方米用于种植A作物，且每平方米产量最大，其余区域按照每平方米10株种植B作物，当这100平方米总产量不低于496千克时，则a的取值范围是 ▲

答案解析收藏纠错 + 选题

15. (2023·大连模拟) 如图，物业公司计划整理出一块矩形绿地，为充分利用现有资源，该矩形绿地一面靠墙（墙的长度为 $\text{[math]}$ ），另外三面用栅栏围成，已知栅栏总长度为 $\text{[math]}$ ，若矩形绿地的面积为 $\text{[math]}$ ，求矩形垂直于墙的一边，即 $\text{[math]}$ 的长．

答案解析收藏纠错 + 选题
16. (2022九上·南昌期中) 如图，在矩形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ．点P沿AB边从点A开始向点B以2cm/s的速度移动，点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（s）表示移动的时间（0≤t≤6）．那么当t为何值时， $\text{[math]}$ 的面积等于8 $\text{[math]}$ ？

答案解析收藏纠错 + 选题
17. (2023·郴州) 随旅游旺季的到来，某景区游客人数逐月增加，2月份游客人数为1.6万人，4月份游客人数为2.5万人．
1. （1）求这两个月中该景区游客人数的月平均增长率；
2. （2）预计5月份该景区游客人数会继续增长，但增长率不会超过前两个月的月平均增长率．已知该景区5月1日至5月21日已接待游客2.125万人，则5月份后10天日均接待游客人数最多是多少万人？
答案解析收藏纠错 + 选题
18. (2023八下·拱墅期中) 如图 $\text{[math]}$ ，用篱笆靠墙围成矩形花圃 $\text{[math]}$ ，一面利用旧墙，其余三面用篱笆围，墙可利用的最大长度为 $\text{[math]}$ ，篱笆长为 $\text{[math]}$ ，设平行于墙的 $\text{[math]}$ 边长为 $\text{[math]}$ ．
1. （1）若围成的花圃面积为 $\text{[math]}$ 时，求 $\text{[math]}$ 的长；
2. （2）如图 $\text{[math]}$ ，若计划在花圃中间用一道篱笆隔成两个小矩形，且花圃面积为 $\text{[math]}$ ，请你判断能否围成花圃，如果能，求 $\text{[math]}$ 的长；如果不能，请说明理由．
答案解析收藏纠错 + 选题
19. (2023九上·永年期中) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，动点P、Q分别以 $\text{[math]}$ ， $\text{[math]}$ 的速度从点A ， C同时出发，沿规定路线移动．
1. （1）若点P从点A移动到点B停止，点Q随点P的停止而停止移动，问经过多长时间P ， Q两点之间的距离是 $\text{[math]}$ ？
2. （2）若点P沿着 $\text{[math]}$ 移动，点Q从点C移动到点D停止时，点P随点Q的停止而停止移动，试探求经过多长时间 $\text{[math]}$ 的面积为 $\text{[math]}$ ？
答案解析收藏纠错 + 选题