(结果精确到0.1cm,参考数据: ,
,
)

如图,塔前有一座高为
的观景台,已知
, 点E,C,A在同一条水平直线上.
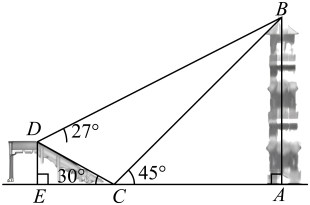
某学习小组在观景台C处测得塔顶部B的仰角为 , 在观景台D处测得塔顶部B的仰角为
.
①用含有h的式子表示线段的长(结果保留根号);
②求塔的高度(
取0.5,
取1.7,结果取整数).
如图1,在正方形中,对角线
相交于点O.在线段
上任取一点P(端点除外),连接
.
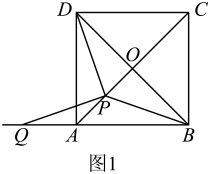
①求证:;
②将线段绕点P逆时针旋转,使点D落在
的延长线上的点Q处.当点P在线段
上的位置发生变化时,
的大小是否发生变化?请说明理由;
③探究与
的数量关系,并说明理由.
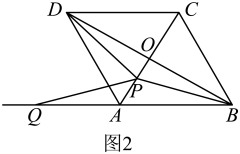
如图2,将正方形换成菱形
, 且
, 其他条件不变.试探究
与
的数量关系,并说明理由.
①如图②,当边与
相交于点M、边
与
相交于点N,且矩形
与菱形
重叠部分为五边形时,试用含有t的式子表示S,并直接写出t的取值范围:
②当时,求S的取值范围(直接写出结果即可).