甲 | 乙 | 丙 |
书A | 书B | 书C |
如图:已知直线 , a⊥b,求证:
.
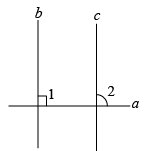
证明:∵(已知),
∴(①垂直的定义).
∵ (已知),
∴(②两直线平行,同位角相等),
∴(③同角的余角相等),
∴(④垂直的定义).
已知:如图,b∥a,c∥a,求证:b∥c; 证明:作直线DF交直线a、b、c分 别于点D、E、F, ∵a∥b,∴∠1=∠4,又∵a∥c, ∴∠1=∠5, ∴b∥c.
|
小明为保证嘉淇的推理更严谨,想在方框中“∴∠1=∠5”和“∴b∥c”之间作补充,下列说法正确的是( )
因为EF∥AD,所以∠2= ,
又因为∠1=∠2,所以∠1=∠3,
所以AB∥ ,
所以∠BAC+ =180°,
因为∠BAC=70°,所以∠AGD= .

已知:如图, , 垂足为A,
.

试说明: .
解:因为(已知),
所以( ).
因为(已知),
所以 ▲ (等量代换).
所以( ).
所以( ).
因为(已知),
所以(垂直的定义).
所以( ).
所以(垂直的定义).
如图,已知∠MAN<45°,点B是射线AM上的一个定点,在射线AN上求作点C,使∠ACB=2∠A.
下面是小路设计的尺规作图过程.
作法:①作线段AB的垂直平分线l,直线l交射线AN于点D;
②以点B为圆心,BD长为半径作弧,交射线AN于另一点C,则点C即为所求.

根据小路设计的尺规作图过程,
证明:连接BD,BC,
∵直线l为线段AB的垂直平分线,
∴DA= ▲ , ( )(填推理的依据)
∴∠A=∠ABD,
∴∠BDC=∠A+∠ABD=2∠A.
∵BC=BD,
∴∠ACB=∠ ▲ , ( )(填推理的依据)
∴∠ACB=2∠A.

解:∵∠BDC=∠A+∠ACD( ▲ ),
∴∠BDC=62°+35°=97°(等量代换).
∵∠BFD+∠BDC+∠ABE= ▲ ( ▲ ),
∴∠BFD=180°﹣∠BDC﹣∠ABE=180°﹣97°﹣20°=63°(等式的性质).