
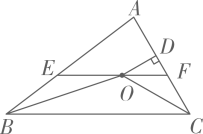

①若AD=BM,则AB=3BD;②AC=BD,则AM=BN;③AC﹣BD=2(MC﹣DN);④2MN=AB﹣CD.
其中正确的结论是( )
![]()


① ,
;
②关于x的方程 的解为
;
③
④ 的值为0或2;
⑤在数轴上点A.B.C表示数a、b、c,若 ,则线段AB与线段BC的大小关系是
.
其中正确的结论是(填写正确结论的序号).
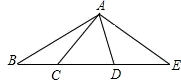

如图1, ,
,
分别是
,
上的点,点
在
,
之间,连接
,
. 用等式表示
,
与
的数量关系.
小刚通过观察,实验,提出猜想: .
接着他对猜想的结论进行了证明,证明思路是:
过点作
, 由
, 可得
, 根据平行线的性质,可得
,
, 从而证得
.

请你利用小刚得到的结论或解题思路,完成下列问题.
已知 ,
,
分别是
,
上的点,点
在
,
之间,连接
,
.
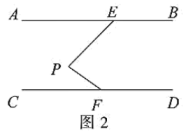


①BE== ;
②∠BAD== ;
③∠AFB==90°;
④S△ABC=.
∵AB∥CD
∴∠1+45°+∠2+45°=.
∴∠1+∠2=.
∴∠E=.
因为M=a+b+c+() = ( ) +3()= 3(),而a、b、k都是整数,所以M可以被三整除.
对于一个数A,以下给出了判断数A是否为19的倍数的一种方法:
每次划掉该数的最后一位数字,将划掉这个数字的两倍与剩下的数相加得到一个和,称为一次操作,依此类推,直到数变为20以内的数为止.若最后得到的数为19.则最初的数A就是19的倍数,否则,数A就不是19的倍数.
以为例,经过第一次操作得到55,经过第二次操作得到15,
,
. 所以436不是19的倍数.
当数A的位数更多时,这种方法依然适用.

当时,请你帮小天写出判断过程;
说明:表示
, 其中
, a,b,c均为整数.
A | A的表达式 | 第一次操作得到的和,记为M(A) |
436 | 436=10×43+6 | M(436)=43+2×6 |
532 | 532= | M(532)= |
863 | 863=10×86+3 | M(863)=86+2×3 |
…… | …… | …… |
| M( |


解: ∵ .(已知)
∴ .()
同理可证, .
∵ ,
∴ .()
应用:如图②, ,点F在
之间,
与
交于点M,
与
交于点N.若
,
,则
的大小为度.
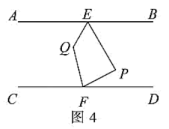
拓展:如图③,直线 在直线
之间,且
,点
分别在直线
上,点Q是直线
上的一个动点,且不在直线
上,连结
.若
,则
=度.