题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /北师大版（2024） /八年级上册 /第三章位置与坐标 /3 轴对称与坐标变化

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

2023-2024学年北师大版数学八年级上册3.3轴对称与坐...

更新时间：2023-08-21 浏览次数：53 类型：同步测试

一、选择题

1. (2024九上·红塔期中) 在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ 关于原点对称的点的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九下·黄石港月考) 如图，在平面直角坐标系中点A的坐标为（3，4），D是△ABC内一点，将△ABC平移得到 $\text{[math]}$ ，平移后点D与其对应点D'关于x轴对称，设点D的坐标为（a，b），则A的对应点 $\text{[math]}$ 的坐标为（）

A . （3，－4） B . （3，4－2b） C . （3，4－2a） D . （－3，4－2b）

答案解析收藏纠错 + 选题
3. (2023八下·乐亭期中) 若点 $\text{[math]}$ ， $\text{[math]}$ 关于x轴对称，则a ， b的值分别为（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·黄冈模拟) 平面直角坐标系中，若点 $\text{[math]}$ 与点 $\text{[math]}$ 关于x轴对称，则点 $\text{[math]}$ 在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
5. (2023八下·嵊州期中) 若点P（a，3）与点Q（-2，b）关于坐标原点对称，则a+b的值为（）

A . 1． B . -1 C . 3 D . -3

答案解析收藏纠错 + 选题
6. (2023九下·柳州月考) 如图，在平面直角坐标系中，△ABC关于直线m（直线m上各点的横坐标都为1）对称，点C的坐标为（4，1），则点B的坐标为（）

A . （-2，1） B . （-3，1） C . （-2，-1） D . （2，1）

答案解析收藏纠错 + 选题
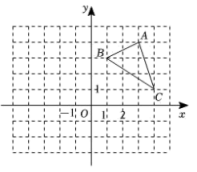
7. (2020·河南模拟) 已知点E（x₀ ， y_o），点F（x₂.y₂），点M（x₁ ， y₁）是线段EF的中点，则x₁＝ $\text{[math]}$ ，y₁＝ $\text{[math]}$ .在平面直角坐标系中有三个点A（1，﹣1），B（﹣1，﹣1），C（0，1），点P（0，2）关于点A的对称点P₁（即P，A，P₁三点共线，且PA＝P₁A），P₁关于点B的对称点P₂ ， P₂关于点C的对称点P₃ ， …按此规律继续以A，B，C三点为对称点重复前面的操作.依次得到点P₄ ， P₅ ， P₆…，则点P₂₀₂₀的坐标是（　　）

A . （4，0） B . （﹣2，2） C . （2，﹣4） D . （﹣4，2）

答案解析收藏纠错 + 选题
8. (2019八上·贵阳月考) 在平面直角坐标系中，对 $\text{[math]}$ 进行循环往复的轴对称变换，若原来点 $\text{[math]}$ 的坐标是 $\text{[math]}$ ，则经过第2019次变换后所得的点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 在平面直角坐标系中，正方形ABCD的顶点分别为A（1，1）.B（1，﹣1）.C（﹣1，﹣1）.D（﹣1，1），y轴上有一点P（0，2）．作点P关于点A的对称点P₁ ，作P₁关于点B的对称点P₂ ，作点P₂关于点C的对称点P₃ ，作P₃关于点D的对称点P₄ ，作点P₄关于点A的对称点P₅ ，作P₅关于点B的对称点P₆┅，按如此操作下去，则点P₂₀₁₁的坐标为（）

A . （0，2） B . （2，0） C . （0，﹣2） D . （﹣2，0）

答案解析收藏纠错 + 选题
10. (2017·岱岳模拟) 如图，在直角坐标系中，矩形OABC的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E，那么点D的坐标为（）

A . （﹣ $\text{[math]}$ ， $\text{[math]}$ ） B . （﹣ $\text{[math]}$ ， $\text{[math]}$ ） C . （﹣ $\text{[math]}$ ， $\text{[math]}$ ） D . （﹣ $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题

二、填空题

11. (2019八上·凉州月考) 已知点M（x，y）与点N（﹣2，﹣3）关于x轴对称，则x+y=．

答案解析收藏纠错 + 选题
12. (2024九下·通榆月考) 已知点 $\text{[math]}$ 与点 $\text{[math]}$ 关于原点对称，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2019·黄陂模拟) 在平面直角坐标系xOy中，已知点P（﹣2，1）关于y轴的对称点P′，点T（t，0）是x轴上的一个动点，当△P′TO是等腰三角形时，t的值是.

答案解析收藏纠错 + 选题
14. (2022八上·雁塔期中) 如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（m，n），则经过第2021次变换后所得的A点坐标是．

答案解析收藏纠错 + 选题
15. (2020九上·林西期末) 如图，在平面直角坐标中，对抛物线 $\text{[math]}$ 在x轴上方的部分进行循环反复的轴对称或中心对称变换，若点A是该抛物线的顶点，则经过第2020次变换后所得的A点的坐标是．

答案解析收藏纠错 + 选题

三、综合题

16. (2023·高明模拟) 点 $\text{[math]}$ 与点 $\text{[math]}$ 在同一平面直角坐标系中．
1. （1）若点 $\text{[math]}$ 位于第四象限，求 $\text{[math]}$ 的取值范围；
2. （2）若点 $\text{[math]}$ 与点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称，求线段 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
17. (2023·雁塔模拟) 如图所示，在平面直角坐标系中，已知 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ；
1. （1）若点 $\text{[math]}$ 与点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称，则点 $\text{[math]}$ 的坐标为；
2. （2）在平面直角坐标系中画出 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的图形 $\text{[math]}$ ；
3. （3）已知 $\text{[math]}$ 为y轴上一点，若 $\text{[math]}$ 的面积为2，直接写出点 $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题
18. (2022七上·咸阳月考) 如图，在平面直角坐标系中， $\text{[math]}$ 的顶点均在网格的格点上，其坐标分别为： $\text{[math]}$ .
1. （1）在图中作出 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的 $\text{[math]}$ ；
2. （2）在(1)的条件下，分别写出点A，C的对应点A₁C₁的坐标.
答案解析收藏纠错 + 选题
19. (2020八上·东城期末) 如图，在平面直角坐标系 $\text{[math]}$ 中，直线l经过点 $\text{[math]}$ ，且平行于y轴给出如下定义：点 $\text{[math]}$ 先关于y轴对称得点 $\text{[math]}$ ，再将点 $\text{[math]}$ 关于直线l对称得点 $\text{[math]}$ ，则称点 $\text{[math]}$ 是点P关于y轴和直线l的二次反射点．
1. （1）已知 $\text{[math]}$ ，则它们关于y轴和直线l的二次反射点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的坐标分别是；
2. （2）若点D的坐标是 $\text{[math]}$ ，其中 $\text{[math]}$ ，点D关于y轴和直线l的二次反射点是点 $\text{[math]}$ ，求线段 $\text{[math]}$ 的长；
3. （3）已知点 $\text{[math]}$ ，点 $\text{[math]}$ ，以线段 $\text{[math]}$ 为边在x轴上方作正方形 $\text{[math]}$ ，若点 $\text{[math]}$ ， $\text{[math]}$ 关于y轴和直线l的二次反射点分别为 $\text{[math]}$ ，且线段 $\text{[math]}$ 与正方形 $\text{[math]}$ 的边有公共点，求a的取值范围．
答案解析收藏纠错 + 选题
20. (2020八上·柳江期中) 如图，在平面直角坐标系中， $\text{[math]}$ .
1. （1）作出 $\text{[math]}$ 关于 $\text{[math]}$ 轴的对称图形 $\text{[math]}$ ；
2. （2）写出点 $\text{[math]}$ 的坐标.
3. （3）在 $\text{[math]}$ 轴上找一点 $\text{[math]}$ ，使 $\text{[math]}$ 的长最短.
答案解析收藏纠错 + 选题

试卷信息