2023年浙教版数学八年级上册5.5一次函数的简单应用同步...

更新时间：2023-10-08 浏览次数：69 类型：同步测试

一、选择题（每题3分，共30分）

1. (2023八下·铜官期末) 不论 $\text{[math]}$ 取何值，点 $\text{[math]}$ 均不在直线 $\text{[math]}$ 上，那么 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九上·新田开学考) 已知一次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 的图象交于点 $\text{[math]}$ .则对于不等式 $\text{[math]}$ ，下列说法正确的是（）

A . 当 $\text{[math]}$ 时， $\text{[math]}$ B . 当 $\text{[math]}$ 时， $\text{[math]}$ C . 当 $\text{[math]}$ 且 $\text{[math]}$ 时， $\text{[math]}$ D . 当 $\text{[math]}$ 且 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·绥棱模拟) 皮克定理是格点几何学中的一个重要定理，它揭示了以格点为顶点的多边形的面积 $\text{[math]}$ ，其中 $\text{[math]}$ 分别表示这个多边形内部与边界上的格点个数．在平面直角坐标系中，横、纵坐标都是整数的点为格点．已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 内部的格点个数是（）

A . 266 B . 270 C . 271 D . 285

答案解析收藏纠错 + 选题
4. (2022·聊城) 如图，一次函数 $\text{[math]}$ 的图象与x轴，y轴分别交于点A，B，点 $\text{[math]}$ 是x轴上一点，点E，F分别为直线 $\text{[math]}$ 和y轴上的两个动点，当 $\text{[math]}$ 周长最小时，点E，F的坐标分别为（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八下·怀化期中) 在密码学中、直接可以看到的内容称为明码，对明码进行某种处理后得到的内容称为密码．有一种密码，将英文26个字母a，b，c，…，z（不分大小写）依次对应1，2，3，…，26这26个自然数（见表格）．当明码对应的序号x为奇数时，密码对应的序号 $\text{[math]}$ ；当明码对应的序号x为偶数时，密码对应的序号 $\text{[math]}$ ．按上述规定，明码和密码相同的序号为（）
字母
a
b
c
d
e
f
g
h
i
j
k
l
m
序号
1
2
3
4
5
6
7
8
9
10
11
12
13
字母
n
o
p
q
r
s
t
u
v
w
x
y
z
序号
14
15
16
17
18
19
20
21
22
23
24
25
26

A . 3 B . 26 C . 3和26 D . 1和26

答案解析收藏纠错 + 选题
6. (2020八下·北京期末) 已知直线 $\text{[math]}$ 过点 $\text{[math]}$ 且与x轴相交夹角为30度，P为直线 $\text{[math]}$ 上一动点， $\text{[math]}$ 为x轴上两点，当 $\text{[math]}$ 时取到最小值时，P的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021八下·越秀期中) 已知直线 $\text{[math]}$ ： $\text{[math]}$ 与直线 $\text{[math]}$ ： $\text{[math]}$ 都经过 $\text{[math]}$ ，直线 $\text{[math]}$ 交y轴于点 $\text{[math]}$ ，交x轴于点A，直线 $\text{[math]}$ 交y轴于点D，P为y轴上任意一点，连接PA、PC，有以下说法：①方程组 $\text{[math]}$ 的解为 $\text{[math]}$ ；② $\text{[math]}$ 为直角三角形；③ $\text{[math]}$ ；④当 $\text{[math]}$ 的值最小时，点P的坐标为 $\text{[math]}$ 其中正确的说法个数有 $\text{[math]}$ $\text{[math]}$

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
8. (2022八上·历下期中) 为培养同学们的创新精神，某校举办校园科技节活动，八年级同学进行了机器人行走性能试验．在试验场地有A，B，C三点顺次在同一笔直的赛道上，甲、乙两机器人分别从A，B两点同时同向出发，历时8分钟同时到达C点，乙机器人始终以60米/分的速度行走，如图是甲、乙两机器人之间的距离y（米）与它们的行走时间x（分钟）之间的函数图象，若前3.5分钟甲机器人的速度不变，则出发（）分钟后两机器人最后一次相距6米．

A . 6 B . 6.4 C . 6.8 D . 7.2

答案解析收藏纠错 + 选题
9. (2021八上·下城期末) 甲，乙两车分别从A， B两地同时出发，相向而行.乙车出发2h后休息，当两车相遇时，两车立即按原速度继续向目的地行驶.设甲车行驶的时间为x(h)，甲，乙两车到B地的距离分别为y₁(km)， y₂(km)， y₁ ， y₂关于x的函数图象如图.下列结论：①甲车的速度是 $\text{[math]}$ km/h；②乙车休息了0.5h；③两车相距a km时，甲车行驶了 $\text{[math]}$ h.正确的是（）

A . ①② B . ①③ C . ②③ D . ①②③

答案解析收藏纠错 + 选题
10. (2023八下·滨海期末) 如图，平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ， $\text{[math]}$ 轴，垂足为 $\text{[math]}$ ，点 $\text{[math]}$ 从原点 $\text{[math]}$ 出发向 $\text{[math]}$ 轴正方向运动，同时，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发向点 $\text{[math]}$ 运动，当点 $\text{[math]}$ 到达点 $\text{[math]}$ 时，点 $\text{[math]}$ 、 $\text{[math]}$ 同时停止运动，若点 $\text{[math]}$ 与点 $\text{[math]}$ 的速度之比为 $\text{[math]}$ ，则下列说法正确的是（）

A . 线段 $\text{[math]}$ 始终经过点 $\text{[math]}$ B . 线段 $\text{[math]}$ 始终经过点 $\text{[math]}$ C . 线段 $\text{[math]}$ 始终经过点 $\text{[math]}$ D . 线段 $\text{[math]}$ 不可能始终经过某一定点

答案解析收藏纠错 + 选题

二、填空题（每空3分，共18分）

11. (2020八上·射阳月考) 如图，将一块等腰直角三角板 ABC放置在平面直角坐标系中， ∠ACB = 90°，AC = BC，点 A在 y轴的正半轴上，点C在 x轴的负半轴上，点 B在第二象限， AC所在直线的函数表达式是 y = x + 2，若保持 AC的长不变，当点 A在 y轴的正半轴滑动，点 C随之在 x轴的负半轴上滑动，则在滑动过程中，点 B与原点 O的最大距离是.

答案解析收藏纠错 + 选题
12. (2019八上·大田期中) 当m，n是正实数，且满足m+n＝mn时，就称点P（m， $\text{[math]}$ ）为“完美点”．已知点A（1，6）与点B的坐标满足y＝﹣x+b，且点B是“完美点”．则点B的坐标是．

答案解析收藏纠错 + 选题
13. (2023八下·重庆市期末) 某日，王艳骑自行车到位于家正东方向的演奏厅听音乐会．王艳离家5分钟后自行车出现故障而且发现没有带钱包，王艳立即打电话通知在家看报纸的爸爸骑自行车赶来送钱包（王艳打电话和爸爸准备出门的时间忽略不计），同时王艳以原来一半的速度推着自行车继续走向演奏厅．爸爸接到电话后，立刻出发追赶王艳，追上王艳的同时，王艳坐上出租车并以爸爸速度的2倍赶往演奏厅（王艳打车和爸爸将钱包给王艳的时间忽略不计），同时爸爸立刻掉头以原速赶到位于家正西方3900米的公司上班，最后王艳比爸爸早到达目的地．在整个过程中，王艳和爸爸保持匀速行驶．如图是王艳与爸爸之间的距离y（米）与王艳出发时间x（分钟）之间的函数图象，则王艳到达演奏厅时，爸爸距离公司米．

答案解析收藏纠错 + 选题

14. (2023·长清模拟) 秤是我国传统的计重工具，为了方便了人们的生活．如图，我们可以用秤砣到秤纽的水平距离得出秤构上所挂物体的重量，称重时，若称杆上秤砣到秤纽的水平距离为x（厘米）时，秤钩所挂物重为y（斤），则y是x的一次函数．下表中为若干次称重时所记录的一些数据．在上表x，y的数据中，发现有一对数据 $\text{[math]}$ 记录不符合题意．当y为7斤时，对应的水平距离为 $\text{[math]}$ ．

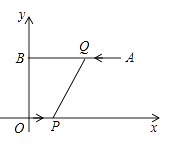
x（厘米）	1	2	4	7	11	12
y（斤）	0.75	1.00	2.00	2.25	3.25	3.50

答案解析收藏纠错 + 选题

15. (2023八上·蒲城期末) 某快递公司每天上午7：00-8：00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数图象如图所示，下列说法：
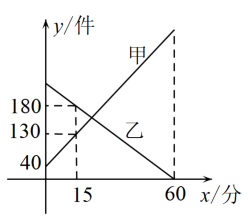
①15分钟后，甲仓库内快件数量为180件；
②乙仓库每分钟派送快件数量为4件；
③8：00时，甲仓库内快件数为600件；
④7：20时，两仓库快递件数相同．
其中正确的个数为．

答案解析收藏纠错 + 选题
16. (2020·重庆模拟) “双11”当天，重庆顺风快递公司出动所有车辆分上午、下午两批往成都送件，该公司共有甲、乙、丙三种车型，其中甲型车数量占公司车辆总数的 $\text{[math]}$ ，乙型车辆是丙型车数量的2倍，上午安排甲车数量的 $\text{[math]}$ ，乙车数量的 $\text{[math]}$ ，丙车数量的 $\text{[math]}$ 进行运输，且上午甲、乙、丙三种车型每辆载货量分别为15吨，10吨，20吨，则上午刚好运完当天全部快件重量的 $\text{[math]}$ ；下午安排剩下的所有车辆运输完当天剩下的所有快件，且下午甲、乙、丙三种车型每辆载货量分别不得超过20吨，12吨，16吨，下午乙型车实际载货量为下午甲型车每辆实际载货量的 $\text{[math]}$ .已知同种货车每辆的实际载货量相等，甲、乙、丙三种车型每辆车下午的运输成本分别为50元/吨，90元/吨，60元/吨.则下午运输时，一辆甲种车、一辆乙种车、一辆丙种车总的运输成本最少为元.

答案解析收藏纠错 + 选题

三、解答题（共9题，共72分）

17. (2023九上·大洼开学考) 为提升学生的文学素养，培养学生的阅读兴趣，某校准备购进A，B两种图书.经调查，购进A种图书费用y元与购进A种图书本数x之间的函数关系如图所示，B种图书每本20元.
1. （1）当 $\text{[math]}$ 和 $\text{[math]}$ 时，求y与x之间的函数关系式；
2. （2）现学校准备购进300本图书，其中购进A种图书x本，设购进两种图书的总费用为w元.
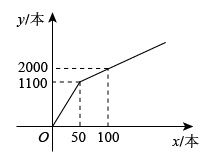
  ①当 $\text{[math]}$ 时，求出w与x间的函数表达式；
  ②若购进A种图书不少于60本，且不超过B种图书本数的2倍，那么应该怎样分配购买A，B两种图书才能使总费用最少？最少总费用多少元？
答案解析收藏纠错 + 选题
18. (2023八下·保定期末) 现从某养殖基地运送144箱鱼苗到 $\text{[math]}$ 、 $\text{[math]}$ 两村养殖，若大、小货车共用14辆，则恰好能一次性运完这批鱼苗，已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往 $\text{[math]}$ 、 $\text{[math]}$ 两村的运费如下表：
养殖基地车型
$\text{[math]}$ 村（元/辆）
$\text{[math]}$ 村（元/辆）
大货车
800
900
小货车
400
600
1. （1）求大、小货车各多少辆？
2. （2）现安排其中10辆货车前往 $\text{[math]}$ 村，其余货车前往 $\text{[math]}$ 村，设前往 $\text{[math]}$ 村的大货车为 $\text{[math]}$ 辆，前往 $\text{[math]}$ 、 $\text{[math]}$ 两村总费用为 $\text{[math]}$ 元，求出 $\text{[math]}$ 与 $\text{[math]}$ 的函数解析式，并直接写出自变量 $\text{[math]}$ 的取值范围；
3. （3）在（2）的条件下，若运往 $\text{[math]}$ 村的鱼苗不少于 $\text{[math]}$ 箱，请写出总费用最少时的货车调配方案，并求出最少费用．
答案解析收藏纠错 + 选题
19. (2023八下·香洲期末) 图中折线表示一骑车人小明离学校的距离 $\text{[math]}$ 与离开学校时间 $\text{[math]}$ 的关系．小明匀速骑行 $\text{[math]}$ 到达图书馆，在图书馆阅读一段时间，然后返回学校；回学校途中，匀速骑行 $\text{[math]}$ 后减速，继续匀速骑行回到学校．请你根据相关信息，解答下列问题：
1. （1）图书馆与学校距离是 $\text{[math]}$ ，小明在图书馆阅读时长为h，小明前往图书馆的平均速度是 $\text{[math]}$ ，当 $\text{[math]}$ 时，y关于x的解析式为；
2. （2）小明刚开始离开学校的时候，另一骑车人小华同时出发，从图书馆沿着相同路线以速度 $\text{[math]}$ 匀速前往学校，到达学校后马上骑车以速度 $\text{[math]}$ 匀速前往图书馆．
  ①请问小华速度 $\text{[math]}$ 为何范围时，小华与小明可以在 $\text{[math]}$ 时相遇；
  ②当 $\text{[math]}$ 时，请求出x为何值时小华与小明相距 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2023八下·铜梁期末) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ，动点F，E分别从点A，B出发，F点沿着 $\text{[math]}$ 运动，到达C点停止运动，点E沿着 $\text{[math]}$ 运动，到达D点停止运动，连接EC，BF，已知F点的速度 $\text{[math]}$ 且 $\text{[math]}$ ，令 $\text{[math]}$ ，运动时间为x．
请回答下列问题：
1. （1）请直接写出 $\text{[math]}$ 与x之间的函数关系式以及对应的x的取值范围；
2. （2）请在直角坐标系中画出 $\text{[math]}$ 的图像，并写出函数 $\text{[math]}$ 的一条性质；
3. （3）根据图形直接估计当 $\text{[math]}$ 时x的取值范围．（结果保留1位小数，误差不超过0.2）
答案解析收藏纠错 + 选题
21. (2023八下·余干期末) 如图，在平面直角坐标系中，已知直线 $\text{[math]}$ ： $\text{[math]}$ 经过 $\text{[math]}$ ，动点 $\text{[math]}$ 在直线 $\text{[math]}$ ： $\text{[math]}$ 上，直线 $\text{[math]}$ 和 $\text{[math]}$ 交于点 $\text{[math]}$ ，设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ，
1. （1）求 $\text{[math]}$ 的值和点 $\text{[math]}$ 的坐标．
2. （2）过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的平行线交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，当以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的四边形为平行四边形时，求 $\text{[math]}$ 的值；
3. （3）过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边向右作正方形 $\text{[math]}$ ，当正方形 $\text{[math]}$ 的顶点 $\text{[math]}$ 或 $\text{[math]}$ 落在直线 $\text{[math]}$ 上时，直接写出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
22. (2023八上·杭州期末) 甲、乙两地相距3000千米，一辆货车和一辆轿车先后从甲地出发驶向乙地，如图，线段 $\text{[math]}$ 表示货车离甲地距离 $\text{[math]}$ 千米 $\text{[math]}$ 与时间 $\text{[math]}$ 小时 $\text{[math]}$ 之间的函数关系；线段 $\text{[math]}$ 表示轿车离甲地距离 $\text{[math]}$ 千米 $\text{[math]}$ 与时间 $\text{[math]}$ 小时 $\text{[math]}$ 之间的函数关系.点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，请根据图象解答下列问题：
1. （1）试求点 $\text{[math]}$ 的坐标；
2. （2）当轿车与货车相遇时，求此时 $\text{[math]}$ 的值；
3. （3）在整个过程中 $\text{[math]}$ ，问 $\text{[math]}$ 在什么范围时，轿车与货车之间的距离小于30千米.
答案解析收藏纠错 + 选题
23. (2017九上·虎林期中) 某天早晨，张强从家跑步去体育锻炼，同时妈妈从体育场晨练结束回家，途中两人相遇，张强跑到体育场后发现要下雨，立即按原路返回，遇到妈妈后两人一起回到家（张强和妈妈始终在同一条笔直的公路上行走）．如图是两人离家的距离y（米）与张强出发的时间x（分）之间的函数图象，根据图象信息解答下列问题：
1. （1）求张强返回时的速度；
2. （2）妈妈比按原速返回提前多少分钟到家？
3. （3）请直接写出张强与妈妈何时相距1000米？
答案解析收藏纠错 + 选题
24. (2023八上·温州期末) 探究通过维修路段的最短时长．
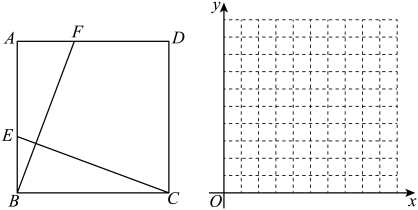
素材1：如图1，某路段(A-B-C-D 段)需要维修，临时变成双向交替通行，故在A，D处各设置红绿灯指导交通(仅设置红灯与绿灯)．

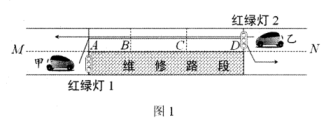
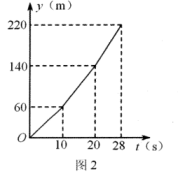
素材2：甲车先由A→D通行，乙车再由D→A通行，甲车经过AB，BC，CD段的时间分别为10s，10s，8s，它的路程y (m)与时间t(s)的关系如图2所示；两车经过BC段的速度相等，乙车经过AB段的速度是10m/s．

素材3：红绿灯1，2每114秒一个循环，每个循环内红灯、绿灯的时长如图3，且每次双向红灯时，已经进入AD段的车辆都能及时通过该路段．

[任务1]求A-B-C-D段的总路程和甲车经过BC段的速度．

[任务2]在图4中补全乙车通过维修路段时行驶的路程y(m)与时间t(s)之间的函数图象．

[任务3]丙车沿NM方向行驶，经DA段的车速与乙车经过时的速度相同，在DN段等红灯的车辆开始行驶后速度为8m/s，等红灯时车流长度每秒增加2m，问丙车在DN段从开始等待至离开点A至少需要几秒钟？

答案解析收藏纠错 + 选题
25. (2023七下·孝义期末) 阅读下列材料，并完成任务．
以方程 $\text{[math]}$ 的解为坐标的点的全体叫做方程 $\text{[math]}$ 的图象．我们知道，二元一次方程 $\text{[math]}$ 有无数组解，我们把每一组解用有序数对 $\text{[math]}$ 表示，就可以描出无数个以方程 $\text{[math]}$ 的解为坐标的点，这无数个点组成一条直线，反过来，这条直线上任意一点的坐标是方程 $\text{[math]}$ 的解．
1. （1）任务一：填空
  ①如图1，在平面直角坐标系中，点 $\text{[math]}$ 是方程 $\text{[math]}$ 的图象上一点，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则方程 $\text{[math]}$ 方程 $\text{[math]}$ 的解．（填“是”或“不是”）
  ②在平面直角坐标系中，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则点 $\text{[math]}$ 方程 $\text{[math]}$ 的图象上．（填“在”或“不在”）
  点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则点 $\text{[math]}$ 方程 $\text{[math]}$ 的图象上．（填“在”或“不在”）
2. （2）任务二：如图2，在平面直角坐标系中，方程 $\text{[math]}$ 的图象与方程 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，则二元一次方程组 $\text{[math]}$ 的解为．
3. （3）任务三：上述用图形的方法得出二元一次方程组的解的过程，主要体现的数学思想是____．（填出下列选项的字母代号即可）
  
  A . 转化思想 B . 数形结合思想 C . 方程思想
答案解析收藏纠错 + 选题