2023年浙教版数学七年级上册5.4一元一次方程的应用同步...

更新时间：2023-10-15 浏览次数：97 类型：同步测试

一、选择题（每题3分，共30分）

1. (2023·海曙竞赛) 如图，在数轴上标出若干点，每相邻两点长为1，P，Q，R，S，T对应的整数分别为p，q，r，s，t，且 $\text{[math]}$ ，则原点对应的点是（）

A . P B . Q C . R D . S

答案解析收藏纠错 + 选题
2. 如图，A，B两地相距1200m，小车从A地出发，以8m/s的速度向B地行驶，中途在C地停靠3分钟.大货车从B地出发，以5m/s的速度向A地行驶，途经D地（在A地与C地之间）时沿原路返回B点取货两次，且往返两次速度都保持不变（取货时间不计），取完两批货后再出发至A点.已知： $\text{[math]}$ ，则直至两车都各自到达终点时，两车相遇的次数为（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
3. (2023七下·义乌开学考) 将 $\text{[math]}$ ， 2， $\text{[math]}$ ， 4，…，60这60个整数分成两组，使得一组中所有数的和比另一组所有数的和小10，这样的分组方法有（）

A . 1种 B . 2种 C . 3种及以上 D . 不存在

答案解析收藏纠错 + 选题
4. (2023七下·开福开学考) 如图，点A在数轴上表示的数是-8，点B在数轴上表示的数是16．若点A以6个单位长度/秒的速度向右匀速运动，同时点B以2个单位长度/秒的速度向左匀速运动．问：当AB＝8时，运动时间为多少秒？（）

A . 2秒 B . 13.4秒 C . 2秒或4秒 D . 2秒或6秒

答案解析收藏纠错 + 选题
5. (2022七下·诸暨期末) 如图，现有3×3的方格，每个小方格内均有数字，要求方格内每一行每一列以及每一条对角线上的三个数字之和均相等，记三个数字之和为P，则P的值为（）

A . 21 B . 24 C . 27 D . 36

答案解析收藏纠错 + 选题
6. (2022八上·余姚期末) 某大型超市购进一批特种水果，运输过程中质量损失 $\text{[math]}$ ，假设不计超市其它费用，如果超市要想至少获得 $\text{[math]}$ 的利润，那么这种水果的售价在进价的基础上应至少提高（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021七上·长沙期末) 如图，数轴上的点O和点A分别表示0和10，点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次，B是线段OA的中点，设点P运动时间为t秒（t不超过10秒）.若点P在运动过程中，当PB＝2时，则运动时间t的值为（）

A . $\text{[math]}$ 秒或 $\text{[math]}$ 秒 B . $\text{[math]}$ 秒或 $\text{[math]}$ 秒或 $\text{[math]}$ 秒或 $\text{[math]}$ 秒 C . 3秒或7秒或 $\text{[math]}$ 秒或 $\text{[math]}$ 秒 D . $\text{[math]}$ 秒或 $\text{[math]}$ 秒或 $\text{[math]}$ 秒或 $\text{[math]}$ 秒

答案解析收藏纠错 + 选题
8. (2022七上·磁县期末) 某超市在“元旦”活动期间，推出如下购物优惠方案：
①一次性购物在 $\text{[math]}$ 元（不含 $\text{[math]}$ 元）以内，不享受优惠；
②一次性购物在 $\text{[math]}$ 元（含 $\text{[math]}$ 元）以上， $\text{[math]}$ 元（不含 $\text{[math]}$ 元）以内，一律享受九折优惠；
③一次性购物在 $\text{[math]}$ 元（含 $\text{[math]}$ 元）以上，一律享受八折优惠；
小敏在该超市两次购物分别付了90 元和270元，如果小敏把这两次购物改为一次性购物，则小敏至少需付款（）元

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022七下·龙岗月考) 某超市为了回馈顾客，若一次性购物不超过300元不优惠，超过300元时按全额9折优惠．一位顾客第一次购物付款180元，第二次购物付款288元，若这两次购物付款合并一次性付款可节省（）

A . 18元 B . 16元 C . 18或46.8元 D . 46.8元

答案解析收藏纠错 + 选题
10. (2021七上·海曙期末) 如图，表中给出的是2021年1月份的月历，任意选取“工”型框中的7个数（如阴影部分所示）．请你运用所学的数学知识来研究，则这7个数的和不可能是（）

A . 76 B . 91 C . 140 D . 16l

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. (2023·宁波竞赛) 某商品随季节变化降价出售，如果按标价降价10%，仍可盈利40元．如果降价后再九折出售，就要亏损14元，则这件商品的标价是元．

答案解析收藏纠错 + 选题
12. (2024七下·河北期末) 在长为 $\text{[math]}$ ，宽为 $\text{[math]}$ （ $\text{[math]}$ ）的长方形纸片上，从它的一侧，剪去一个以长方形纸片宽为边长的正方形（第一次操作）；从剩下的长方形纸片一侧再剪去一个以宽为边长的正方形（第二次操作）；按此方式，如果第三次操作后，剩下的纸片恰为正方形，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

13. (2022七上·瑞安期中) 下表是某市居民出行方式以及收费标准：（不足1千米按1千米算）

打车方式	出租车	3千米以内8元；超过3千米的部分2.4元/千米
打车方式	滴滴快车	路程：1.4元/千米；时间：0.6元/分钟
说明	打车的平均车速40千米/时

假设乘坐8千米，耗时：8÷40×60＝12分钟；出租车收费：8＋（8－3）×2.4＝20元；滴滴快车收费：8×1.4＋12×0.6＝18.4元．

为了提升市场竞争力，出租车公司推出行使里程超过10千米立减4.8元活动．小聪乘坐出租车从甲地到达乙地支付车费22.4元，若改乘滴滴快车从甲地到乙地，则需支付元．

答案解析收藏纠错 + 选题

14. (2022七下·重庆市月考) 茶百道生产的一种由A、B两种原料按一定比例配制而成的奶茶，其中A原料成本价为10元/千克，B原料成本价为15元/千克，按现行价格销售每千克奶茶可获得4.8元的利润.由于物价上涨，A原料上涨20%，B原料上涨10%，配制后的总成本增加 $\text{[math]}$ .茶百道为了拓展市场，打算再投入现总成本的10%做广告宣传，使得销售成本再次增加，如果要保证每千克的利润不变，则此时这种奶茶每千克的售价与原售价之差为元

答案解析收藏纠错 + 选题
15. (2023七上·义乌月考) 将长为4宽为a（a大于1且小于4）的长方形纸片按如图所示的方式折叠并压平，剪下一个边长等于长方形宽的正方形，称为第一次操作；再把剩下的长方形按同样的方式操作，称为第二次操作；如此反复操作下去，若在第n次操作后，剩下的长方形恰为正方形，则操作终止.当 $\text{[math]}$ 时，a的值为.

答案解析收藏纠错 + 选题
16. (2022七上·衢江期末) 实验室里有一个水平放置的正方体容器，从内部量得它的棱长为15cm，容器内的水深为4cm、现往容器内放入如图所示的长方体实心铁块（铁块一面平放在容器底面），过顶点A的三条棱的长分别10cm，10cm，xcm（x<15）．
1. （1）容器内水的体积为 cm³
2. （2）当铁块的顶部高出水面1cm时，x的值为．
答案解析收藏纠错 + 选题

三、解答题（共8题，共72分）

17. (2022七上·江油月考) 由甲地到乙地前三分之二的路是高速公路，后三分之一的路是普通公路，高速公路和普通公路交界处是丙地． $\text{[math]}$ 车在高速公路上的行驶速度是 $\text{[math]}$ ，在普通公路上的行驶速度是 $\text{[math]}$ ； $\text{[math]}$ 车在高速公路上的行驶速度是 $\text{[math]}$ ，在普通公路上的行驶速度是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 两车分别从甲，乙两地同时出发相向行驶．在高速公路上距离丙地 $\text{[math]}$ 处相遇，求甲，乙两地之间的距离是多少？

答案解析收藏纠错 + 选题
18. (2023七下·长泰期中) 如图，在长方形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点M以 $\text{[math]}$ 的速度从点A出发，沿 $\text{[math]}$ 的路线运动，点N以 $\text{[math]}$ 的速度从点D出发，沿 $\text{[math]}$ 的路线运动.若点M，N同时出发，当点N回到点D时，M，N两点同时停止运动.运动时间为t（s）.
1. （1）当t为何值时，点M，N在运动路线上相遇；
2. （2）当t为何值时，点M，N在运动路线上相距的路程为 $\text{[math]}$ ；
3. （3）在整个运动过程中，是否存在直线 $\text{[math]}$ 把长方形分成两个梯形，且这两个梯形的面积比为 $\text{[math]}$ ，若存在，求出t的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题

19. (2023七上·温州期末) 根据以下素材，探索完成任务．

如何设计宣传牌？
素材1	如图1是长方形宣传牌，长330cm，宽220cm，拟在上面书写24个字． (1)中间可以用来设计的部分也是长方形，且长是宽的1.55倍． (2)四周空白部分的宽度相等．
素材2	如图2，为了美观，将设计部分分割成大小相等的左、中、右三个长方形栏目，栏目与栏目之间的中逢间距相等．
素材3	如图3，每栏划出正方形方格，中间有十字间隔，竖行两列中间间隔和横向中间间隔宽度比为1：2．

问题解决
任务1	分析数量关系	设四周宽度为xcm，用含x的代数式分别表示设计部分的长和宽．
任务2	确定四周宽度	求出四周宽度x的值．
任务3	确定栏目大小	(1)求每个栏目的水平宽度． (2)求长方形栏目与栏目之间中缝的间距．

答案解析收藏纠错 + 选题

20. (2023七上·金东期末) 盲盒近来火爆，其主打“盲”，盒子上不会标注里面是什么，只有打开才会知道，有越多惊喜，所以深受中学生的喜爱.寒假将近，胡老师准备网购以下两款盲盒若干个，作为新年礼物奖励给班里有学习进步的同学.

类型	介绍	图片	单价
文具盲盒	里面可能包含笔袋、中性笔、笔记本、手账本、便签、胶带等各种学习用品，能开出什么文具，纯凭个人手气.		10元/个
Molly盲盒	泡泡玛特是国内最火的盲盒品牌，而Molly则被称为“泡泡玛特一姐”，一个系列有12个不同Molly造型，也有可能会抽到隐藏款哦.		59元/个

（1）若胡老师网购两种盲盒共40个，花费792元，则两种盲盒各采购了多少个？

（2）为清理库存，文具盲盒店家现推出优惠活动：

购买数量	每个售价
前10个	标价
第11个到第20个	标价的九折
第21个到第30个	标价的八折
超过30个	标价的七折

此时正巧碰上电商平台的年货节，在该商店打完折的基础上，还可以享受电商平台的优惠：每满200-25（即总价在200元到399元可以优惠少付25元；总价400元到599元可以优惠少付50元；总价600元到799元可以优惠少付75元；）

①若胡老师购买了35个文具盲盒，应付给该商家多少钱？

②若胡老师购买文具盲盒共花费181元，则她购买了几个文具直盒？

答案解析收藏纠错 + 选题

21. (2023七上·恩平期末) 将连续的自然数1到150按图1的方式排列成一个方阵：
1. （1）在图1中，第6行的第3个数是，第20行的最后一个数是；
2. （2）如图2，用一个正方形在该方阵中任意框出9个数，请用代数方法说明这9个数之和一定是9的倍数；
3. （3）如图3，若用如图所示的长方形在该方阵中任意框出6个数，这6个数之和能等于156吗？如果能，请求出这6个数；如果不能，请说明理由．
答案解析收藏纠错 + 选题

22. (2023七上·江北期末) 小江同学注意到妈妈手机中的电费短信（如下左图），对其中的数据产生了浓厚的兴趣，谷 $\text{[math]}$ 度是什么意思?电费是如何计算的?第一档与第二档又有什么关系？

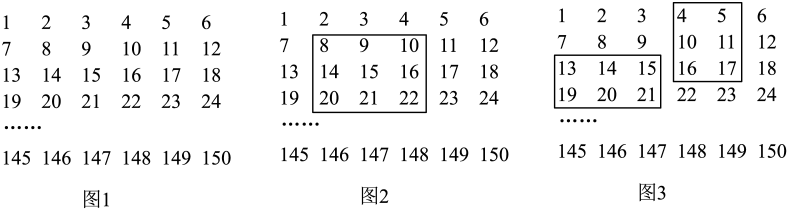
表1：宁波市居民生活用电标准（部分修改）

电压等级		普通电价（元/度）	峰谷电价（元/度）
电压等级		普通电价（元/度）	峰时电价	谷时电价
第一档	年用电量不超过2760度的部分	0.538	0.568	0.288
第二档	年用电量超过2760度但不超过4800度的部分	0.588	0.618	0.338
第三档	年用电量超过4800度的部分	0.838	0.868	0.588

【解读信息】

通过互联网查询后获得上表（如表1）.小江家采用峰谷电价计费，谷时用电量为85度，那么峰时用电量就是 $\text{[math]}$ 度，由于小江家年用电量处在第一档，故9月份电费为： $\text{[math]}$ .

第一档年用电量的上限为2760度，所以截至9月底小江家已经用电2760－581＝2179度.不难发现，第二档所有电价均比第一档提高0.05元/度，第三档所有电价均比第一档提高0.3元/度.

【理解信息】

（1）若采用普通电价计费，小江家九月份的电费为元.（精确到 $\text{[math]}$ ）
（2）若采用峰谷电价计费，假设某月谷时用电量与月用电量的比值为m，那么处在第一档的1度电的电费可以表示成元.（用含有m的代数式表示）
（3）【重构信息】
12月份，小江家谷时用电量与月用电量的比值为0.2.请根据上述对话完成下列问题：

①通过计算判断：截至12月底小江家的年用电量是否仍处于第一档？

②12月份谁家的用电量多，多了多少？

答案解析收藏纠错 + 选题

23. (2021七上·太原期末) 阅读材料，解答下列问题：

幻方历史悠久，传说最早出现在夏禹时代的“洛书”（如图1）把图1的洛书用今天的数学符号翻译出来，就是一个三阶幻方，如图2，它的每行、每列、每条对角线上的三个数的和都和等．

（1）在图2中，每行、每列、每条对角线上三个数的和为；
（2）设图3所示的三阶幻方中间的数为x（x为整数），请用含x的代数式将图3幻方补充完整；
（3）从A，B两题中任选一题作答．我选择 ▲ 题．
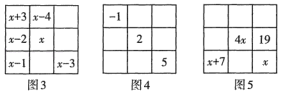
A．将－2，－1，0，1，2，3，4，5，6这9个数中除－1，2，5外的6个数填入图4中其余的方格中，使其成为一个三阶幻方．
B．如图5是一个三阶幻方，按方格中已给的信息，x的值为 ▲ ， 4x上方的方格中的数为 ▲ ．

答案解析收藏纠错 + 选题

24. (2022七上·余姚竞赛) 【阅读理解】
若A，B，C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点C是[A，B]的“妙点”．例如，如图1，点A表示的数为-1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是[A，B]的“妙点”.又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是[A，B]的“妙点”，但点D是[B，A]的“妙点”．

【知识应用】

如图2，M、N为数轴上两点，点M所表示的数为-2，点N所表示的数为4．
1. （1）数3(填“是”或“不是”）[M，N]的“妙点”，数2(填“是”或“不是”）[N，M]的“妙点”.
2. （2）若数轴上有一点Q表示的数是x，且点Q是[N，M]的妙点，求x的值.
3. （3）如图3，A、B为数轴上两点，点A所表示的数为-40，点B所表示的数为20．现有一只电子蚂蚁P从点B出发，以2个单位每秒的速度向左运动，到达点A停止．当t为何值时，点P，A和B中恰有一个点为其余两点的“妙点”？（请直接写出答案）
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中