

 B .
B .  C .
C .  D .
D . 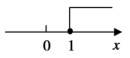
 B .
B .  C .
C .  D .
D . 
|
x |
… |
1 |
2 |
4 |
5 |
6 |
8 |
9 |
… |
|
y |
… |
3.92 |
1.95 |
0.98 |
0.78 |
2.44 |
2.44 |
0.78 |
… |
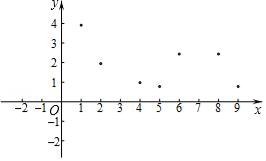
小风根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象和性质进行了探究.
下面是小风的探究过程,请补充完整:
①x=7对应的函数值y约为多少;
②写出该函数的一条性质.

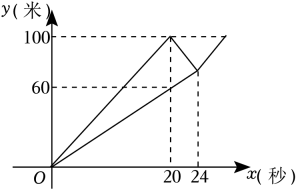
如图①,将长为的铅笔
斜靠在垂直于水平桌面
的直尺
的边沿上,一端
固定在桌面上,图②是示意图.
如图③,将铅笔绕端点
顺时针旋转,
与
交于点
, 当旋转至水平位置时,铅笔
的中点
与点
重合.
设 , 点
到
的距离
.
数学思考:
