 B .
B .  C .
C .  D .
D . 
甲:当时,该方程没有实数根;
乙:当时,该方程有两个相等实数根;
丙:当时,该方程有两个不相等的实数根.

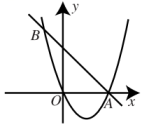


① ②
若此函数的图象为直线,则此函数的图象经过
;
若此函数的图象为抛物线,且经过
, 则该抛物线开口向下;
若此函数的解析式为
, 且经过原点,则
;
若此函数的解析式为
, 开口向下,且
, 则
的范围是
.
所有合理推断的序号是 .

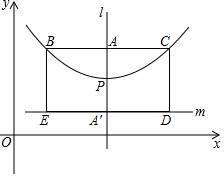
②直接写出抛物线y=(x-3)2+2的焦点矩形与抛物线y=x2-2mx+m2+1有两个公共点时m的取值范围.
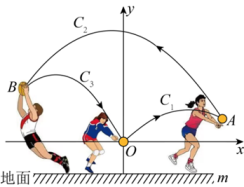
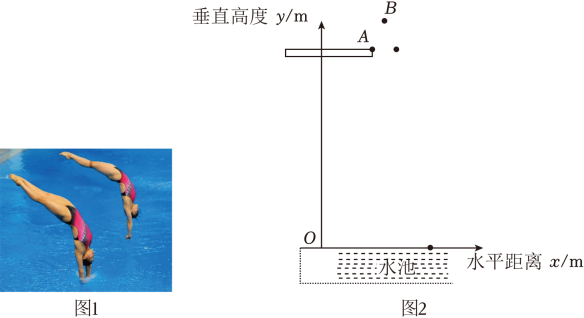
水平距离x/m | 0 | 3 | 3.5 | 4 | 4.5 |
竖直高度y/m | 10 | 10 | k | 10 | 6.25 |
根据上述数据,直接写出k的值为 ,直接写出满足的函数关系式:;
写出该函数的一条性质:;
方程
的解为:;
若方程
有四个实数根,则
的取值范围是.
将函数的图象经过怎样的平移可得到函数
的图象?写出平移过程,并直接写出当
时,自变量
的取值范围.
问题情境
小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉,为了确定售价,小莹帮妈妈调查了附近A,B,C,D,E五家花卉店近期该种盆栽花卉的售价与日销售量情况,记录如下:
售价(元/盆) | 日销售量(盆) | |
A | 20 | 50 |
B | 30 | 30 |
C | 18 | 54 |
D | 22 | 46 |
E | 26 | 38 |
请将以上调查数据按照一定顺序重新整理,填写在下表中:
|
售价(元/盆) |
|||||
|
日销售量(盆) |
分析数据的变化规律,找出日销售量与售价间的关系;
根据以上信息,小莹妈妈在销售该种花卉中,
①要想每天获得400元的利润,应如何定价?
②售价定为多少时,每天能够获得最大利润?