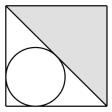
 B .
B . 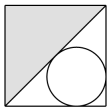 C .
C . 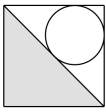 D .
D . 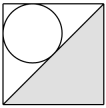
 C .
C . 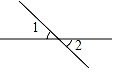 D .
D . 
①相等的角是对顶角
②经过一点有且只有一条直线与已知直线平行
③两条直线被第三条直线所截,同位角相等
④直线外一点到这条直线的垂线段的长度叫做点到直线的距离
⑤过一点有且只有一条直线与已知直线垂直
其中真命题有( )
参赛者 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 14 | 6 | 64 |

如图,已知AB∥EF , EP⊥EQ , ∠1+∠APE=90°,求证:AB∥CD .
证明:∵AB∥EF ,
∴∠APE= ▲ ( ).
∵EP⊥EQ ,
∴∠PEQ= ▲ ( ).
即∠2+∠3=90°.
∴∠APE+∠3=90°.
∵∠1+∠APE=90°,
∴∠1= ▲ .
∴ ▲ ∥CD( ).
又∵AB∥EF ,
∴AB∥CD( ).
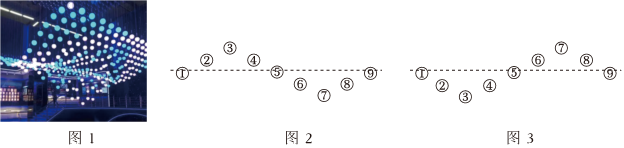
为了丰富社会实践活动,引导学生科学探究.学校组织七年级同学走进中国科技馆.亲近科学,感受科技魅力,来到科技馆大厅,同学们就被大厅里会“跳舞”的“小球矩阵”吸引住了(如图1).白色小球全部由计算机精准控制,每一只小球可以“悬浮”在大厅上空的不同位置,演绎着曲线、曲面、平面、文字和三维图案等各种动态造型.
已知每个小球分别由独立的电机控制.图2,图3分别是9个小球可构成的两个造型,在每个造型中,相邻小球的高度差均为a米.为了使小球从造型一(如图2)变到造型二(如图3),控制电机使造型一中的②,③,④,⑥,⑦,⑧号小球同时运动,②,③,④小球向下运动,运动速度均为4米/秒;⑥,⑦,⑧号小球向上运动,运动速度均为3米/秒.当每个小球到达造型二的相应位置时就停止运动.已知⑦号小球比②号小球晚秒到达相应位置,问②号小球运动了多少米?

收购A或B的数量(单位:箱 | 不超过30箱 | 超过30箱 |
优惠方式 | 收购总价打九五折 | 收购总价打八折 |
第一次收购了两个品种共60箱,且收购的B品种箱数比A品种箱数多;受某些因素影响,蔬菜商人第二次收购时做出了价格调整:每箱A的收购价不变,每箱B的收购价比第一次的收购价降低 , 优惠方式不变.两次收购完所有的黑马铃薯后,蔬菜商人发现第二次支付给老李的费用比第一次支付给老李费用多11400元,求蔬菜商人第一次收购A品种黑马铃薯多少箱?