其中能用“两点之间,线段最短”来解释的现象有( )
 B .
B .  C .
C .  D .
D . 

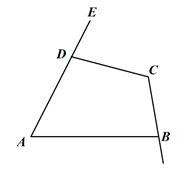
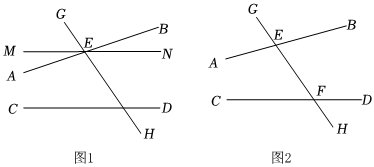
①如图1,三角板的一边与射线
重合,且
, 若以点
为观察中心,射线
表示正北方向,求射线
表示的方向;
②如图2,将三角板放置到如图位置,使恰好平分
, 且
, 求
的度数.


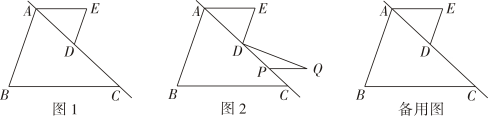
①如图2所示,当DE⊥DQ时,求∠Q的度数.
②在整个运动过程中,当∠Q=2∠EDQ时,求∠Q的度数.
①如果两个数的绝对值相等,那么这两个数的平方相等;②内错角相等;③在同一平面内,垂直于同一条直线的两条直线互相平行;④两个无理数的和一定是无理数;⑤坐标平面内的点与有序数对是一一对应的.其中真命题的个数是( )
对于方案Ⅰ、Ⅱ,说法正确的是( )
方案Ⅰ:作一直线
, 交
、
于点
,
;
利用尺规作
;
测量
的大小即可.
方案Ⅱ:作一直线
, 交
、
于点
,
;
测量
和
的大小;
计算
即可.
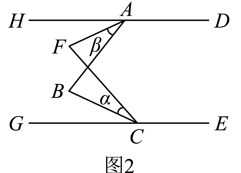
已知:如图,直线 ,
被直线
所截,
.
对说明理由.

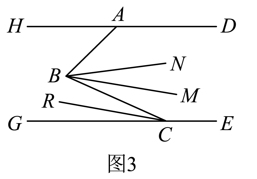
方法 如图, |
方法 如图, |
下列说法正确的是( )