
在一次数学实践探究活动中,大家遇到了这样的问题:
如图,在一个圆柱体形状的包装盒的底部A处有一只壁虎,在顶部B处有一只小昆虫,壁虎沿着什么路线爬行,才能以最短的路线接近小昆虫?
楠楠同学设计的方案是壁虎沿着A﹣C﹣B爬行;
浩浩同学设计的方案是将包装盒展开,在侧面展开图上连接AB,然后壁虎在包装盒的表面上沿着AB爬行.
在这两位同学的设计中,哪位同学的设计是最短路线呢?他们的理论依据是什么?( )

①用剪刀沿着它的棱剪开这个纸盒,至少要剪7刀,才能展开成平面图形;②用一平面去截这个正方体得到的截面是三角形ABC,则∠ABC=45°;③一只蚂蚁在一个实心正方体木块P点处想沿着表面爬到C点最近的路只有4条;④用一平面去截这个正方体得到的截面可能是八边形;⑤正方体平面展开图有11种不同的图形.

⑴若将图1中正方体的表面沿某些棱剪开,展成一个平面图形,需要剪开7条棱;
⑵用一个平面从不同方向去截图1中的正方体,得到的截面可能是三角形、四边形、五边形或六边形;
⑶用一个平面去截图1中的正方体得到图2,截面三角形ABC中∠ABC=45°;
⑷如图3,要搭成该几何体的正方体的个数最少是a,最多是b,则a+b=19
其中正确结论的个数有( )

【阅读】|5﹣2|表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;|5+2|可以看做|5﹣(﹣2)|,表示5与﹣2的差的绝对值,也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.
![]()
实践与操作:在射线AM上作线段AB=a,AC=a-b.(要求:尺规作图,保留作图痕迹,不写作法)
![]()
推理与探究:若线段AB的中点是点D,线段BC的中点是点E,请在上图中标出点D,E.探究:线段DE与AC有怎样的数量关系,并说明理由.
规律发现:
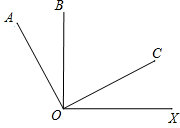
度;
度;
度.
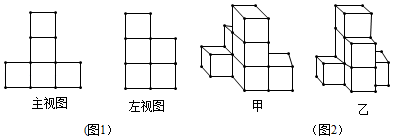
①这个几何体可能是(图2)甲、乙中的;
②这个几何体最多可由个小正方体构成,请在图3中画出符合最多情况的一个俯视图.
①画线段AB,射线AD;
②找一点M,使M点即在射线AD上,又在直线BC上;
③找一点N,使N到A、B、C、D四个点的距离和最短.

拓展探究:如图②,∠AOB=α,∠AOC=β.(α,β为锐角),射线OM平分∠BOC,ON平分∠AOC.求∠MON的度数;
迁移应用:其实线段的计算与角的计算存在着紧密的联系,如图③线段AB=m,延长线段AB到C,使得BC=n,点M,N分别为AC,BC的中点,则MN的长为 ▲ (直接写出结果).

![]()
① 表示的点与数表示的点重合;
② 若数轴上A、B两点之间距离为9(A在B的左侧),且A、B两点经折叠后重合,此时点A表示的数是,点B表示的数是.

①若 , 则线段DE的长为cm.
②设 , 则线段DE的长为cm.
将∠COD绕着顶点O顺时针继续旋转如图(3)位置,若∠BOC=45°,射线OE在∠BOC内部,且∠BOC=3∠BOE.请探究:
①∠BOC的补角有 ▲ 个,分别是 ▲ ;
②求∠DOE的度数.
如图(1)所示,若∠AOB=58°,求∠BOC的度数;
折叠长方形纸片,OC,OD均是折痕,折叠后,点A落在点A′,点B落在点B′,连接OA′.如图(2)所示,当点B′在OA′上时,判断∠AOC与∠BOD的关系,并说明理由;
如图(3)所示,在图(2)的基础上,当点B′在∠COA′的内部时,连接OB′.若∠AOC=44°,∠BOD=61°,求∠A′OB′的度数.
如图②,直线l上有两个点M , N , 且 . 若点P是点M关于点N的“半距点”,则
.
点M和点N在数轴上对应的数分别为m、n , 且 , 点W是线段
的中点,P、Q两点分别从点M和N同时出发,沿数轴作匀速运动,点P的速度是每秒1个单位,点Q的速度是每秒3个单位
若点P向右运动,点Q向左运动,在点K相遇,试判断点K是否是点M关于点W的“半距点”,并请说明理由.
①若 , 则线段
的长为
;
②设 , 则线段
的长为
.
在此基础上,我们给出如下定义:比较与
的大小,若
, 则将其中较小角的度数定义为
对
的“迷你角度”;若
, 则将
或
的度数定义为
对
的“迷你角度”.
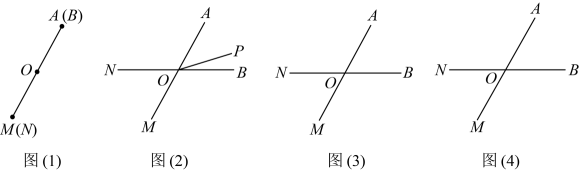
①如图(2)所示,若 , 求
对
的“迷你角度”是多少度;
②若对
的“迷你角度”为
, 请借助图(3)和图(4)进行分析,求出
的值是多少.
①如图1,当射线OC在∠AOB外部,∠BOC=40°时,求∠EOD的度数;
②当∠BOC=α()时,则∠EOD的度数是 ▲ ;
①当∠BOC=40°,OC位置如图2所示时,求∠EOD的度数.
②当∠BOC=α时(0°<α<180°),则∠EOD的度数是 ▲ .

请你借助三角尺完成以下画图,并标注所使用三角尺的相应角度.
实验目的:了解钟面上时针与分针在转动时的内在联系,学会用一元一次方程解决钟面上的有关数学问题,体会数学建模思想.
实验准备:机械钟(手表)一只
实验内容与步骤:
①时针每分钟转动 °,分针每分钟转动 .
②从3点整到3点20分,分针转动的角度为 °.
①若时间为2:30,则钟面角为 °(钟面角是时针与分针所成的夹角).
②1点整到3点整之间,钟面角为90°的情况有 种.
晚上七点刚过,小强开始做数学作业,一看时钟,发现此时时针和分针在同一直线上,他做完作业,八点不到,此时,时针和分针又在同一直线上,则小强做数学作业花了多少时间?(直接写出答案)
①请计算出这个几何体的体积;
②如果在这个几何体上再添加一些相同的正方体纸盒,并保持从上面看到的形状和从左面看到的形状不变,最多可以再添加 个正方体纸盒.