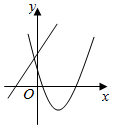 B .
B . 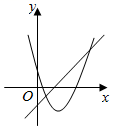 C .
C . 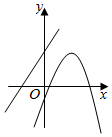 D .
D . 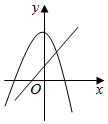
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣11 | ﹣5 | ﹣1 | 1 | 1 | … |


x(元/件) | 40 | 50 | 60 |
y(件) | 10000 | 9500 | 9000 |


①抛物线y=-x2+4关于x轴的矢高是,跨径是,矢跨比是;
②有一抛物线经过点c,与抛物线y=-x2+4开口方向与大小一样,且矢高是抛物线y=-x2+4关于x轴的矢高的 , 求它关于x轴的矢跨比;

