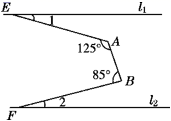


请你参考小敏同学的方法,解决下面问题:


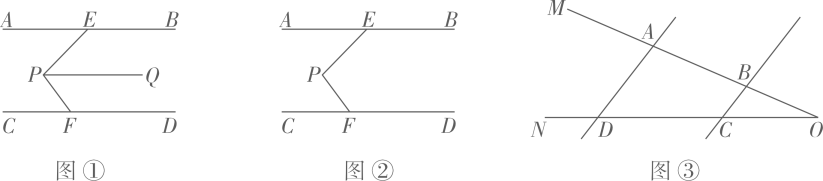
小明:老师说在解决有关平行线的问题时,如果无法直接得到角的关系,就需要借助辅助线来帮助解答,今天老师介绍了一个“美味”的模型一“猪蹄模型”.即

已知:如图1, ,
为
、
之间一点,连接
,
得到
.
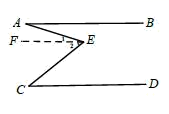
求证:
小明笔记上写出的证明过程如下:
证明:过点 作
,
∴
∵ ,
∴
∴ .
∵
∴
请你利用“猪蹄模型”得到的结论或解题方法,完成下面的两个问题.
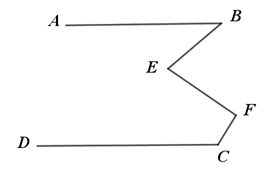
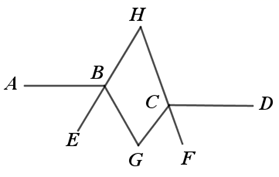
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1 ,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2 ,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3 , …,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En .
若∠En=1度,那∠BEC等于度

请你在小颖操作探究的基础上,继续完成下面的问题:
(ⅰ)猜想图中
与
之间的数量关系并加以证明;
(ⅱ)补全图 , 直接写出
与
之间的数量关系: ▲ .


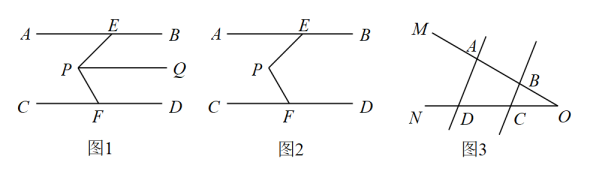
与例4条件和结论互换,改成了:“如图1,AP 平分∠BAC,CP平分∠ACD,AB∥CD,则∠1+∠2=90°,”小明认为这个结论正确,你赞同他的想法吗? 请说明理由.
小明发现:若将其中一条角平分线改成AC的垂线,则“∠1+∠2=90°”这个结论不成立.请帮小明完成探究:
如图2,AB∥CD,AP平分∠BAC,CP⊥AC,∠1是AP与AB的夹角,∠2 是CP与CD的夹角.
①若∠2=22°,求∠1的度数.
②试说明:2∠1-∠2=90°.
如图3,若AB∥CD,AP⊥AC,CP平分∠ACD,请直接写出∠1与∠2的数量关系.