2023-2024学年北师大版八年级下学期数学期中仿真模拟卷...

更新时间：2024-04-15 浏览次数：148 类型：期中考试

一、选择题（每题3分，共30分）

1. (2023九上·南昌期中) 下列图案中，不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024八下·巴彦期中) 以下列线段的长为三边的三角形中，能构成直角三角形的是（）

A . 3² ， 4² ， 5² B . 13，5，12 C . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023八上·西湖月考) 已知等腰三角形的两条边长分别为2和5，则它的周长为（）

A . 9 B . 12 C . 9或12 D . 5

答案解析收藏纠错 + 选题
4. (2023八下·长安期中) 如图，在等腰 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 垂直平分 $\text{[math]}$ ，则 $\text{[math]}$ 的度数等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八下·伊川期中) 观察图中尺规作图痕迹，下列结论不正确的是（）

A . $\text{[math]}$ 为 $\text{[math]}$ 的平分线 B . $\text{[math]}$ C . 点A、B到 $\text{[math]}$ 的距离不相等 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八下·埇桥期中) 下列式子：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ ；⑥ $\text{[math]}$ ，你认为其中是不等式的有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题
7. (2023八下·光明期中) 一次函数 $\text{[math]}$ 与 $\text{[math]}$ 在同一平面直角坐标系内的图象如图所示，则不等式组 $\text{[math]}$ 的解集为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 以上答案都不对

答案解析收藏纠错 + 选题
8. (2024八下·温县期中) 若关于x的不等式组 $\text{[math]}$ 的整数解共有2个，则m的取值范围是（）

A . 5<m≤6 B . 4<m≤5 C . 5≤m<6 D . 4≤m<5

答案解析收藏纠错 + 选题
9. (2023八下·交城期中) 如图是楼梯的示意图，楼梯的宽为5米， $\text{[math]}$ 米， $\text{[math]}$ 米，若在楼梯上铺设防滑材料，则所需防滑材料的面积至少为（）

A . 65 $\text{[math]}$ B . 85 $\text{[math]}$ C . 90 $\text{[math]}$ D . 150 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023八下·青原期末) 如图，在第一个△ABA₁中，∠B=20°，AB=A₁B，在A₁B上取一点C，延长AA₁到A₂ ，使得A₁A₂=A₁C，得到第二个△A₁A₂C；在A₂C上取一点D，延长A₁A₂到A₃ ，使得A₂A₃=A₂D；…，按此做法进行下去，则第5个三角形中，以点A₄为顶点的等腰三角形的底角的度数为（）

A . 5° B . 10° C . 15° D . 25°

答案解析收藏纠错 + 选题

二、填空题（每题3分，共15分）

11. (2022八下·南湖期中) 用反证法证明“直角三角形中至少有一个锐角小于或等于45°”，应先假设.

答案解析收藏纠错 + 选题
12. (2024八下·锦江月考) 若关于x的不等式 $\text{[math]}$ 可化为 $\text{[math]}$ ，则a的取值范围是．

答案解析收藏纠错 + 选题
13. (2023八下·佛冈期中) 某商场店庆活动中，商家准备对某种进价为 $\text{[math]}$ 元、标价为 $\text{[math]}$ 元的商品进行打折销售，但要保证利润率不低于 $\text{[math]}$ ，则最多打折 $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2023八下·惠来期中) 如图，一个含有30°角的三角板ABC，绕点B顺时针旋转到 $\text{[math]}$ 的位置，使A，B， $\text{[math]}$ 在同一条直线上，则旋转角的度数为.

答案解析收藏纠错 + 选题
15. (2022八下·清城期中) 如图，△ABC为等边三角形，边长为6，AD⊥BC，垂足为点D，点E和点F分别是线段AD和AB上的两个动点，连接CE，EF，则BE＋EF的最小值为．

答案解析收藏纠错 + 选题

三、解答题（共9题，共75分）

16. (2023八下·珠山期中) 解不等式组 $\text{[math]}$ 并把解集表示在数轴上．

答案解析收藏纠错 + 选题
17. (2023八下·珠山期中) 如图，在由边长为1的小正方形组成的正方形网格中， $\text{[math]}$ 的顶点均在格点上．
1. （1）画出 $\text{[math]}$ 关于原点成中心对称的 $\text{[math]}$ ．
2. （2）画出 $\text{[math]}$ 绕点C逆时针旋转 $\text{[math]}$ 得到的 $\text{[math]}$ ．
3. （3）在x轴上是否存在一点P，使得 $\text{[math]}$ 的周长最小？若存在，直接写出点P的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
18. (2022八下·河东期中) 图①是用硬纸板做成的两个全等的直角三角形，两条直角边的长分别为a和b，斜边为c．图②是以c为直角边的等腰直角三角形．请你开动脑筋，将它们拼成一个直角梯形．
1. （1）画出拼成的这个图形的示意图，并标注相关数据；
2. （2）利用（1）中画出的图形证明勾股定理．
答案解析收藏纠错 + 选题
19. (2022八下·合浦期中) 在△ABC中，AB＝AC，CD⊥AB于D.
1. （1）若∠A＝40°，求∠DCB的度数；
2. （2）若BC＝15，CD＝12，求AC的长.
答案解析收藏纠错 + 选题
20. (2023八下·莲湖期中) 如图，已知△ABC为等边三角形．P为△ABC内一点，PA＝8，PB＝6，PC＝10，若将△PBC绕点B逆时针旋转后得到△P′BA．
1. （1）求点P与点P′之间的距离；
2. （2）求∠APB的度数．
答案解析收藏纠错 + 选题
21. (2022八下·巴州期中) 阅读下列内容，设a， b， c是一个三角形的三条边的长，且a是最长边，我们可以利用a， b， c三边长间的关系来判断这个三角形的形状；
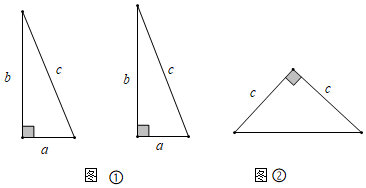
①若 $\text{[math]}$ 则该三角形是直角三角形②若 $\text{[math]}$ ，则该三角形是钝角三角形；③ $\text{[math]}$ ；则该三角形是锐角三角形

例如一个三角形的三边长分别是4，5，6则最长边是6， $\text{[math]}$ ，故由上面③可知该三角形是锐角三角形，请解答以下问题
1. （1）若一个三角形的三条边长分别是2，3，4，则该三角形是三角形
2. （2）若一个三角形的三条边长分别是3，4，x且这个三角形是直角三角形则x的值为
3. （3）若一个三角形的三条边长分别为 $\text{[math]}$ ，mn， $\text{[math]}$ ，请判断这个三角形的形状，并写出你的判断过程.
答案解析收藏纠错 + 选题
22. (2022八下·太原期中) 下面是小颖证明命题“在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半”的过程，请阅读后完成相应任务．
已知：如图1， $\text{[math]}$ 中， $\text{[math]}$ ．
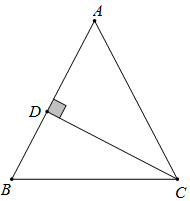
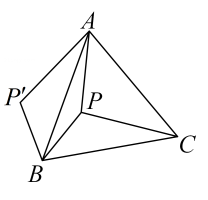
求证：____
证明：延长BC到点D，使 $\text{[math]}$ ，连接AD．
∵ $\text{[math]}$ ，
∴ $\text{[math]}$
∵ $\text{[math]}$ ，
∴ $\text{[math]}$ ． ∴ $\text{[math]}$ ．
∴ $\text{[math]}$ 是等边三角形．（依据：____）
∴ $\text{[math]}$ ， ∴ $\text{[math]}$ ．
1. （1）上述过程中，求证的结论为；括号中的依据为；
2. （2）证明以上命题后，小颖运用它解决了下列问题．
  请从A，B两题中任选一题补全图形并作答．我选择题．
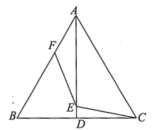
  如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ，点E是AB的中点．
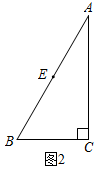
  A．过点E作EF垂直于AC，垂足为点F，求EF的长．
  B．过点E作EF垂直于AB，垂足为点E，交AC于点F，求EF的长．
答案解析收藏纠错 + 选题
23. (2023八下·石家庄期中) 为了丰富学生的生活，拓宽学生的视野，提高学生各方面的能力，某校组织八年级全体学生共540人前往某社会实践基地开展研学活动，学校若租用8辆A型客车和4辆B型客车，则恰好全部坐满，已知每辆A型客车的乘客座位数比B型客车多12个．
1. （1）求每辆A型客车和每辆B型客车的乘客座位数．
2. （2）为确保研学活动能够更好地展开与记录，每辆车上需有1名教师同行，学校决定调整租车方案．已知租用一辆A型客车的费用为2100元，租用一辆B型客车的费用为1500元．在保持租用车辆总数不变的情况下，为接载所有参加活动的师生，如何租用车辆可使得租车总费用最少，并求租车总费用的最小值．
答案解析收藏纠错 + 选题
24. (2023八下·通州期中) 在平面直角坐标系 $\text{[math]}$ 中，对于点 $\text{[math]}$ 和点 $\text{[math]}$ ，给出如下定义：如果 $\text{[math]}$ 且 $\text{[math]}$ （k为正整数），那么称点P为点M关于坐标轴的“k倍距”．
1. （1） ①在点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，点为原点O关于坐标轴的“1倍距”；
  ②如果点P在函数 $\text{[math]}$ 的图象上，且为原点O关于坐标轴的“2倍距”，求b的取值范围．
2. （2）如果直线 $\text{[math]}$ 上存在点 $\text{[math]}$ 是点 $\text{[math]}$ 关于坐标轴的“2倍距”，直接写出m的取值范围．
答案解析收藏纠错 + 选题