题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

2024年江苏省淮安市中考数学仿真模拟卷

更新时间：2024-05-09 浏览次数：46 类型：中考模拟

一、选择题（每题3分，共24分）

1. (2024七下·北京市期中) 下列各数中的无理数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024·广东模拟) 下列图形中，既是轴对称图形是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024·北京市模拟) 原子钟是以原子的规则振动为基础的各种守时装置的统称，其中氢脉泽钟的精度达到了1700000年误差不超过1秒.数据1700000用科学记数法表示（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·定远期中) 下列式子中，计算正确的是（）

A . a³+a³＝a⁶ B . （﹣a²）³＝﹣a⁶ C . a²•a³＝a⁶ D . （a+b）²＝a²+b²

答案解析收藏纠错 + 选题
5. (2024九下·黄石月考) 实数a ， b ， c在数轴上对应的点如图所示，下列判断正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八下·印江月考) 如图，将一副三角板在平行四边形ABCD中作如下摆放，设 $\text{[math]}$ ，那么 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024·德阳模拟) 已知某几何体的三视图（单位：cm）如图所示，则该几何体的侧面积和侧面展开图圆心角的度数为（　　）

A . 12πcm²和215° B . 15πcm²和216° C . 24πcm²和217° D . 30πcm²和218°

答案解析收藏纠错 + 选题
8. (2024·广东模拟) 如图，在平面直角坐标系中，直线y=-3x+3交x轴于点A，交y轴于点B，以AB为边在第一象限作正方形ABCD，其中顶点D恰好落在双曲线y=k/x上，现将正方形ABCD沿y轴向下平移a个单位长度，可以使得顶点C落在双曲线上，则a的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题3分，共24分）

9. (2024八下·凉州期中) 使根式 $\text{[math]}$ 有意义的x的取值范围是．

答案解析收藏纠错 + 选题
10. (2024九下·肇庆月考) 分式方程 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
11. (2021·建湖模拟) 若一条长为32cm的细线能围成一边长等于8cm的等腰三角形，则该等腰三角形的腰长为cm.

答案解析收藏纠错 + 选题
12. (2024七下·碑林月考) 已知 $\text{[math]}$ ，代数式 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024·金华模拟) 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数均是9.2环，方差分别为 $\text{[math]}$ ，则这四人中成绩最稳定的是.

答案解析收藏纠错 + 选题
14. (2023·宣州模拟) 如图， $\text{[math]}$ 是直径，点B、C、D在半圆上，若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024·威远模拟) 如图，四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，满足 $\text{[math]}$ ，则 $\text{[math]}$ 面积的最小值为．

答案解析收藏纠错 + 选题
16. (2023·龙江模拟) 矩形 $\text{[math]}$ 的边 $\text{[math]}$ ．点 $\text{[math]}$ 为平面内一点， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题（共11题，共102分）

17. (2024八下·西安月考) 已知关于x ， y的方程组 $\text{[math]}$ 的解满足不等式 $\text{[math]}$ ，求m的负整数解．

答案解析收藏纠错 + 选题
18. (2023·广元模拟) 先化简，再求值： $\text{[math]}$ ，其中x满足方程 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2024·四平模拟) 已知：如图，点D在△ABC的BC边上，AC∥BE，BC=BE，∠ABC=∠E，求证：AB=DE．

答案解析收藏纠错 + 选题
20. (2024九下·沭阳模拟) 有4张正面分别写有数字1，2，3，4的不透明卡片，它们除数字外完全相同，将它们背面朝上洗匀.
1. （1）随机抽取一张，求抽到数字为奇数的概率.
2. （2）随机抽取两张，记下两张卡片的数字，用列表或画树状图求抽取的两张卡片上数字之和为奇数的概率.
答案解析收藏纠错 + 选题
21. (2024·武汉模拟) “惜餐为荣，殄物为耻”，为了解落实“光盘行动”的情况，某校调研了七、八年级部分班级某一天的餐后垃圾质量．从七、八年级各随机抽取10个班餐后垃圾质量的数据（单位： $\text{[math]}$ ），进行整理和分析（餐后垃圾质量用x 表示，共分为四个等级：A． $\text{[math]}$ ；B． $\text{[math]}$ ；C． $\text{[math]}$ ；D． $\text{[math]}$ ），下面给出了部分信息．
七年级10个班餐后垃圾质量： $\text{[math]}$ ．
八年级10个班餐后垃圾质量中B 等级包含的所有数据为： $\text{[math]}$ ．
七八年级抽取的班级餐后垃圾质量统计表
年级
平均数
中位数
众数
方差
A等级所占百分比
七年级
$\text{[math]}$
$\text{[math]}$
a
$\text{[math]}$
$\text{[math]}$
八年级
$\text{[math]}$
b
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
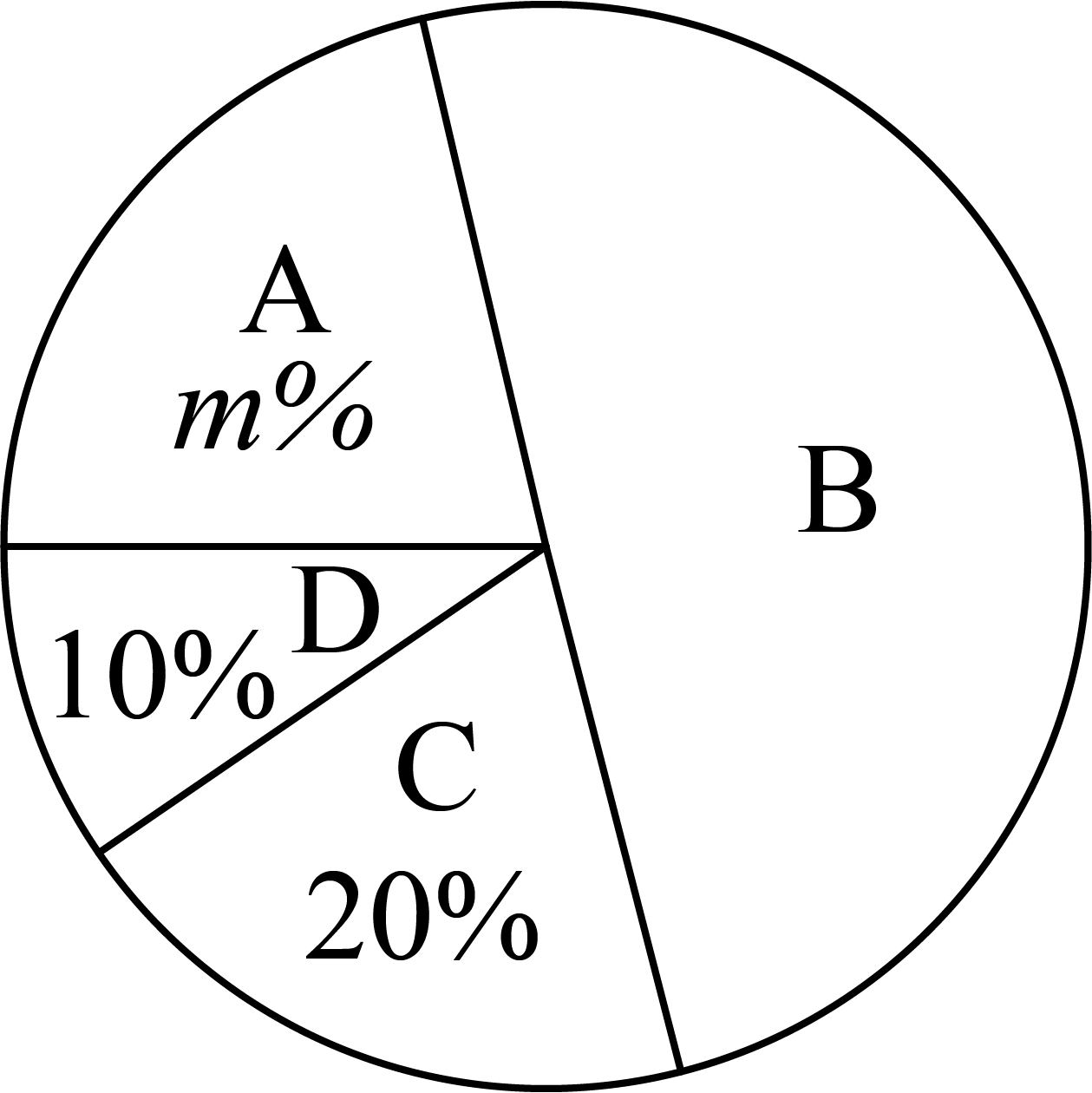
八年级抽取的班级餐后垃圾质量扇形统计图
1. （1）直接写出上述表中a，b，m 的值；
2. （2）该校八年级共有30个班，估计八年级这一天餐后垃圾质量符合A 等级的班级数；
3. （3）根据以上信息，你认为该校七、八年级的“光盘行动”，哪个年级落实得更好？请说明理由（写出一条理由即可）．
答案解析收藏纠错 + 选题
22. (2023·武功模拟) 如图，某小区矩形绿地的长宽分别为30m，20m．现计划对其进行扩充，将绿地的长、宽增加相同的长度后，得到一个新的矩形绿地．若扩充后的矩形绿地面积为 $\text{[math]}$ ，求新的矩形绿地的长与宽．

答案解析收藏纠错 + 选题
23. (2024·化州模拟) 如图，小华和同伴秋游时，发现在某地小山坡的点E处有一棵小树，他们想利用皮尺、倾角器和平面镜测量小树到山脚下的距离（即DE的长度），小华站在点B处，让同伴移动平面镜至点C处，此时小华在平面镜内可以看到点E．且测得BC＝3米，CD＝28米．∠CDE＝127°．已知小华的眼睛到地面的距离AB＝1.5米，请根据以上数据，求DE的长度．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
24. (2024·拱墅模拟) 学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地．两人之间的距离y（米）与时间t（分钟）之间的函数关系如图所示．
1. （1）根据图象信息，求出甲和乙的速度各为多少？（单位：米/分钟）
2. （2）求线段AB所在的直线的函数表达式；
3. （3）在整个过程中，请通过计算，t为何值时两人相距400米？
答案解析收藏纠错 + 选题
25. (2024九下·广州月考) 如图“ $\text{[math]}$ 字形” $\text{[math]}$ ， $\text{[math]}$ ，
1. （1）作 $\text{[math]}$ 的角平分线 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，作出线段 $\text{[math]}$ 的中点 $\text{[math]}$ ．（要求：尺规作图，保留作图痕迹，不必写出作法）
2. （2）利用三角尺过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径作圆．
  ①判断 $\text{[math]}$ 与直线 $\text{[math]}$ 的位置关系，并说明理由；
  ②连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的半径．
答案解析收藏纠错 + 选题
26. (2024·温州模拟) 已知二次函数 $\text{[math]}$ ．
1. （1）若它的图象经过点 $\text{[math]}$ ，求该函数的对称轴．
2. （2）若 $\text{[math]}$ 时，y的最小值为1，求出t的值．
3. （3）如果 $\text{[math]}$ ， $\text{[math]}$ 两点都在这个二次函数的图象上，直线 $\text{[math]}$ 与该二次函数交于 $\text{[math]}$ ， $\text{[math]}$ 两点，则 $\text{[math]}$ 是否为定值？若是，请求出该定值：若不是，请说明理由．
答案解析收藏纠错 + 选题
27. (2024·南山模拟) “转化”是解决数学问题的重要思想方法，通过构造图形全等或者相似建立数量关系是处理问题的重要手段．
1. （1）【问题情景】：如图 $\text{[math]}$ ，正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 是线段 $\text{[math]}$ 上一点 $\text{[math]}$ 不与点 $\text{[math]}$ 、 $\text{[math]}$ 重合 $\text{[math]}$ ，连接 $\text{[math]}$ 将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
  以下是两名同学通过不同的方法构造全等三角形来解决问题的思路，
  ①小聪：过点 $\text{[math]}$ 作 $\text{[math]}$ 的延长线的垂线；
  ②小明：在 $\text{[math]}$ 上截取 $\text{[math]}$ ，使得 $\text{[math]}$ ；
  请你选择其中一名同学的解题思路，写出完整的解答过程．
2. （2）【类比探究】：如图 $\text{[math]}$ 点 $\text{[math]}$ 是菱形 $\text{[math]}$ 边 $\text{[math]}$ 上一点 $\text{[math]}$ 不与点 $\text{[math]}$ 、 $\text{[math]}$ 重合 $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，使得 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为 $\text{[math]}$ 用含 $\text{[math]}$ 的代数式表示 $\text{[math]}$ ．
3. （3）【学以致用】：如图 $\text{[math]}$ ，在 $\text{[math]}$ 的条件下，连结 $\text{[math]}$ ，与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，当 $\text{[math]}$ 时，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题

试卷信息