2024年广东省深圳市中考数学全真模拟试卷(六)

更新时间：2024-07-03 浏览次数：80 类型：中考模拟

一、选择题(本题共10小题，每小题3分，共30分，每题有4个选项同，只有一个正确)

1. (2024七下·江海期中) 在实数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， 9中，无理数有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
2. (2024七上·海曙期末) “春江潮水连海平，海上明月共潮生”，水是诗人钟爱的意象，经测算，一个水分子的直径约为 $\text{[math]}$ ，数据 $\text{[math]}$ 用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七下·珠海期中) 下列所示的图案分别是奔驰、雪铁龙、大众、三菱汽车的车标，其中可以看作由“基本图案”经过平移得到的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024七下·珠海期中) 如图，过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形是三角板)，其依据是（）

A . 同旁内角互补，两直线平行 B . 两直线平行，同旁内角互补 C . 同位角相等，两直线平行 D . 两直线平行，同位角相等

答案解析收藏纠错 + 选题
5. (2024九上·朝阳月考) 下列判断不正确的是（）

A . 若 $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ，则 $\text{[math]}$ D . 若 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八下·义乌月考) 在《代数学》中记载了求方程x²+8x＝33正数解的几何方法：如图1，先构造一个面积为x²的正方形，再以正方形的边为一边向外构造四个面积为2x的矩形，得到大正方形的面积为33+16＝49，则该方程的正数解为7﹣4＝3．小明尝试用此方法解关于x的方程x²+10x+c＝0时，构造出如图2所示正方形．已知图2中阴影部分的面积和为39，则该方程的正数解为（）

A . 2 $\text{[math]}$ B . 2 C . 3 D . 4 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024七下·贵州期中) 如图是一盏可调节台灯及其示意图．固定支撑杆 $\text{[math]}$ 垂直底座 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 是分别可绕点 $\text{[math]}$ 和 $\text{[math]}$ 旋转的调节杆，台灯灯罩可绕点 $\text{[math]}$ 旋转调节光线角度，在调节过程中，最外侧光线 $\text{[math]}$ 、 $\text{[math]}$ 组成的 $\text{[math]}$ 始终保持不变．现调节台灯，使外侧光线 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024·四平模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径且 $\text{[math]}$ ，点 $\text{[math]}$ 在圆上且 $\text{[math]}$ ， $\text{[math]}$ 的平分线交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ 并过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，则弦 $\text{[math]}$ 的长度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023九上·光明月考) 如图，在正方形ABCD中，E，F是对角线AC上的两点，且EF＝2AE＝2CF，连接DE并延长交AB于点M，连接DF并延长交BC于点N，连接MN，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024九下·新兴模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的内接三角形，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题(此题共5小题，每小题3分，共15分)

11. (2024·锦江模拟) 分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2024八下·义乌月考) 某招聘考试分笔试和面试两种，小明笔试成绩90分，面试成绩85分，如果笔试成绩、面试成绩按3：2计算，那么小明的平均成绩是分

答案解析收藏纠错 + 选题
13. (2019九上·重庆开学考) 某超市以A、B两种糖果为原料，组装出了甲、乙、丙三种糖果礼盒（礼盒包装成本忽略不计）.其中，甲礼盒每盒含1千克A糖果、1千克B糖果；乙礼盒每盒含2千克A糖果、1千克B糖果；丙礼盒每盒含1千克A糖果、3千克B糖果.甲礼盒每盒售价48元，利润率为20%.国庆节期间，该超市进行打折促销活动，将甲、乙、丙礼盒各一盒合组装成大礼包，并且每购买一个大礼包可免费赠送一个乙礼盒，这样即可实现利润率为30%，则每个大礼包的售价为元.

答案解析收藏纠错 + 选题
14. (2024九下·温州开学考) 如图，在平面直角坐标系中，矩形ABCD的顶点A，B在x轴的正半轴上，反比例函数 $\text{[math]}$ 的图象经过顶点D，分别与对角线AC，边BC交于点E，F，连接EF，AF．若点E为AC的中点，△AEF的面积为2，则k的值为.

答案解析收藏纠错 + 选题
15. (2024九上·宁波期末) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ 为 $\text{[math]}$ 的中点，
$\text{[math]}$ 的延长线与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题(共7小题，共55分，其中第16题6分，第17题、第18题7分，第19题、第20题8分，第21题9分，第22题10分)

16. (2024·娄底模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2024九下·黄石月考) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024九下·澄海模拟) 今年3月25日是第29个全国中小学生安全教育日．某市面向中小学生举行了一次关于心理健康、预防欺凌、防溺水、应急疏散等安全专题知识竞赛，共有18000名学生参加本次竞赛．为了解本次竞赛成绩情况，随机抽取了n名学生的成绩x（成绩均为整数，满分为100分）分成四个组：1组（ $\text{[math]}$ ），2组（ $\text{[math]}$ ），3组（ $\text{[math]}$ ），4组（ $\text{[math]}$ ），并绘制如图所示频数分布图．
1. （1） $\text{[math]}$ ；所抽取的n名学生成绩的中位数在第组；
2. （2）若成绩在第4组才为优秀，则所抽取的n名学生中成绩为优秀的频率为；
3. （3）试估计18000名参赛学生中，成绩大于或等于70分的人数．
答案解析收藏纠错 + 选题

19. (2024八下·义乌期中) 根据以下素材，探索完成任务．

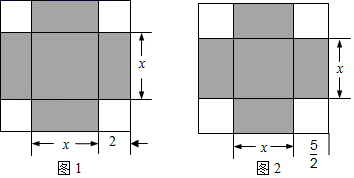
素材1	某校统一安装了日光灯，日光灯中最易损坏的是灯管和镇流器．
素材2	该校后勤部准备补进灯管和镇流器共400件．批发市场灯管的单价为30元，镇流器的单价为80元．商家为了促销且保证有一定的利润，当镇流器购买数量超过80件时，每多购买1件，单价下降1元，但单价不低于50元．
问题解决
任务1	若镇流器补进90件，则学校补进镇流器和灯管共多少元？
任务2	设镇流器补进x件，若 $\text{[math]}$ ，刚补进镇流器的单价为 ▲ 元，补进灯管的总价为 ▲ （用含x的代数式表示）；
任务3	若学校后勤部补进镇流器和灯管共花15000元，求补进镇流器多少件？

答案解析收藏纠错 + 选题

20. (2019·哈尔滨模拟) 如图是形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，请在图a、b中分别画出符合要求的图形，所画图形各顶点必须在格点上；
1. （1）画一个底边长为4，面积为8的等腰三角形；
2. （2）画一个面积为10的等腰直角三角形．
答案解析收藏纠错 + 选题

21. (2024九下·深圳期中)

根据背景素材，探索解决问题．

生活中的数学——自动旋转式洒水喷头如何灌溉草坪
背景素材	数学来源于生活，九4班分四个小组，开展数学项目式实践活动，获取所有数据共享，对草坪喷水管建立数学模型．草坪装有1个自动旋转式洒水喷头，灌溉园林草坪．如图1所示，观察喷头可顺、逆时针往返喷洒．

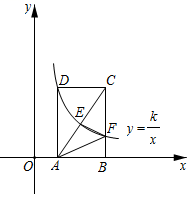
	甲小组在图2中建立合适的直角坐标系，喷水口中心O有一喷水管OA ，从A点向外喷水，喷出的水柱最外层的形状为抛物线．以水平方向为x轴，点O为原点建立平面直角坐标系，点A（喷水口）在y轴上，x轴上的点D为水柱的最外落水点．	乙小组在甲小组基础上，测量得距洒水喷头水平距离较远若干米的E处，正上方有一树枝叶F ，旋转式喷洒水柱外端刚好碰到树叶F的最低处．
	丙小组在甲小组基础上，测量得喷水口中心O到水柱的最外落水点D距离为半径，建立⊙O半径为OD的扇形平面图（图3）.
问题解决
任务1	获取数据	丁小组测量得喷头的高 $\text{[math]}$ 米，喷水口中心点O到水柱的最外落水点D水平距离为8米，经过点 $\text{[math]}$ ．
	解决问题	求出水柱所在抛物线的函数解析式．
任务2	获取数据	丁小组测树叶F距水平地面最低高度 $\text{[math]}$ 米，点F在抛物线上且离水喷头水平距离较远，E在OD上，OD⊥EF ．
	解决问题	求OE的长．
任务3	推理计算	丁小组观察自动旋转式洒水喷头可顺、逆时针往返喷洒，可平面旋转角度不超过240°，求： ①这个喷头最多可洒水多少平方米？ ②在①条件下，此时DD^'的长．

答案解析收藏纠错 + 选题

22. (2023·天河模拟) 综合与探究
在矩形ABCD的CD边上取一点E ，将△BCE沿BE翻折，使点C恰好落在AD边上的点F处.
1. （1）如图①，若BC＝2BA ，求∠CBE的度数；
2. （2）如图②，当AB＝5，且AF•FD＝10时，求EF的长；
3. （3）如图③，延长EF ，与∠ABF的角平分线交于点M ， BM交AD于点N ，当NF＝AN+FD时，请直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2024年广东省深圳市中考数学全真模拟试卷(六)

副标题：

*注意事项：

2024年广东省深圳市中考数学全真模拟试卷(六)

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析