命题新趋势3 真实情境（1）——2024年浙教版数学八（下）...

更新时间：2024-06-03 浏览次数：42 类型：复习试卷

一、二次根式

1. (2024八下·余杭月考) 高空抛物极其危险，是我们必须杜绝的行为．据研究，高空抛物下落的时间 $\text{[math]}$ （单位：s）和高度h（单位：m）近似满足公式 $\text{[math]}$ （不考虑风速的影响）．记从 $\text{[math]}$ 高空抛物到落地所需时间为 $\text{[math]}$ ．从 $\text{[math]}$ 高空抛物到落地所需时间为 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
2. 如图，已知钓鱼竿AC的长为6 m，露在水面上的渔线BC长为3 $\text{[math]}$ m，某钓鱼者想看看鱼钩上的情况，把鱼竿AC转动到AC'的位置，此时露在水面上的渔线B'C'为 $\text{[math]}$ m，则BB'的长为（）

A . $\text{[math]}$ m B . 2 $\text{[math]}$ m C . $\text{[math]}$ m D . 2 $\text{[math]}$ m

答案解析收藏纠错 + 选题
3. (2024八下·长兴月考) 如图①是一张等腰直角三角形纸片， $\text{[math]}$ ，现要求按照图②的方法裁剪几条宽度都为 $\text{[math]}$ 的长方形纸条，用这些纸条为一幅正方形美术作品EFGH镶边(纸条不重叠)如图③，正方形美术作品的面积为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
4. (2023八下·瑞安期中) 有一块长方形木板，木工采用如图所示的方式，在木板上截出两个面积分别为18dm²和32dm²的正方形木板，则剩余木料(阴影部分)的面积为dm² ．

答案解析收藏纠错 + 选题
5. (2024八下·嵊州月考) 如图，有一张面积为 $\text{[math]}$ 的正方形纸板，现将该纸板的四个角剪掉，制作一个有底无盖的长方体盒子，剪掉的四个角是面积相等的小正方形，此小正方形的边长为 $\text{[math]}$ ．
1. （1）求长方体盒子的容积；
2. （2）求这个长方体盒子的侧面积．
答案解析收藏纠错 + 选题
6. (2024八下·鄞州期中) 小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如： $\text{[math]}$ ，善于思考的小明利用完全平方公式进行了以下探索：
$\text{[math]}$ ．请你仿照小明的方法解决下列问题：
1. （1） $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）已知x是4- $\text{[math]}$ 的算数平方根，求 $\text{[math]}$ +2x-2024的值；
3. （3）当1 $\text{[math]}$ x $\text{[math]}$ 2时，化简 $\text{[math]}$
答案解析收藏纠错 + 选题
7. 某太阳能热水器的横截面示意图如图所示，已知真空热水管 $\text{[math]}$ 与支架 $\text{[math]}$ 所在的直线相交于点 $\text{[math]}$ ，且 $\text{[math]}$ ，支架 $\text{[math]}$ 与水平线 $\text{[math]}$ 垂直， $\text{[math]}$ ， $\text{[math]}$ ．求：
1. （1）支架 $\text{[math]}$ 的长．
2. （2）真空热水管 $\text{[math]}$ 的长． (结果保留根号)
答案解析收藏纠错 + 选题
8. (2024八下·慈溪期中) 数学老师在课堂上提出一个问题：“通过探究知道： $\text{[math]}$ ，它是无限不循环小数，也叫无理数，它的整数部分是1，那么有谁能说出它的小数部分是多少”，王英举手回答：它的小数部分我们无法全部写出来，但可以用 $\text{[math]}$ 来表示它的小数部分，张老师夸奖王英真聪明，肯定了她的说法．现请你根据王英的说法解答下列问题：
1. （1）请表示出 $\text{[math]}$ 的小数部分；
2. （2）若a为 $\text{[math]}$ 的小数部分，b为 $\text{[math]}$ 的整数部分，求 $\text{[math]}$ 的值；
3. （3）已知 $\text{[math]}$ ，其中x是一个正整数， $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
9. 如图，一艘船想从 $\text{[math]}$ 处行驶至河对岸最近点 $\text{[math]}$ 处．由于水流的影响，实际靠岸地点 $\text{[math]}$ 偏离 $\text{[math]}$ 处 $\text{[math]}$ ，这艘船实际行驶的路程AC为 $\text{[math]}$ ．求该河的宽度AB（结果保留根号）．

答案解析收藏纠错 + 选题
10. (2024八下·长兴月考) 阅读材料：
已知a，b为非负实数， $\text{[math]}$
$\text{[math]}$ ，当且仅当“ $\text{[math]}$ ”时，等号成立.
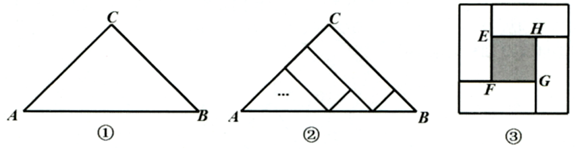
这个结论就是著名的“均值不等式”，“均值不等式”在一类最值问题中有着广泛的应用.
例：已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 最小值.
解：令 $\text{[math]}$ ，则由 $\text{[math]}$ ，得 $\text{[math]}$ .
当且仅当 $\text{[math]}$ ，即 $\text{[math]}$ 时，代数式取到最小值，最小值为6.
根据以上材料解答下列问题：
1. （1）【灵活运用】
  已知 $\text{[math]}$ ，则当 $\text{[math]}$ 时，代数式 $\text{[math]}$ 取到最小值，最小值为.
2. （2）已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的最小值.
3. （3）【拓展运用】
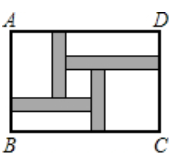
  某校要对操场的一个区域进行改造，利用一面足够长的墙体将该区域用围栏围成中间隔有两道围栏的矩形花圃，如图1所示，为了围成面积为 $\text{[math]}$ 的花圃，所用的围栏至少为多少米?
4. （4）如图2，四边形ABCD的对角线AC，BD相交于点 $\text{[math]}$ 和 $\text{[math]}$ 的面积分别是4和12，求四边形ABCD面积的最小值.
答案解析收藏纠错 + 选题

二、一元二次方程

11. (2024八下·绍兴期中) 如图，在一块长为 $\text{[math]}$ ，宽为 $\text{[math]}$ 的矩形 $\text{[math]}$ 空地内修建四条宽度相等，且与矩形各边垂直的道路.四条道路围成的中间部分恰好是一个正方形，且边长是道路宽的4倍，道路占地总面积为 $\text{[math]}$ .设道路宽为 $\text{[math]}$ ，则以下方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024八下·西湖月考) 目前我国建立了比较完善的经济困难学生资助体系，某校2021年给贫困学生每人400元补贴，2023年给贫困学生每人560元补贴，设每年发放的资助金额的平均增长率为x，则下面列出的方程中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2024八下·温州经济技术开发月考) 某校在操场东边开发出一块长、宽分别为 $\text{[math]}$ 、 $\text{[math]}$ 的矩形菜园（如图），作为劳动教育系列课程的实验基地之一．为了便于管理，现要在中间开辟一横两纵三条等宽的小道，剩下的用于种植，且种植面积为 $\text{[math]}$ ．设小道的宽为 $\text{[math]}$ ，根据题意可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
14. 某医疗物资制造厂原来每件产品的生产成本是100元，为提高生产效率改进了生产技术，连续两次降低成本后，成本是81元，则平均每次降低成本的百分率为（）

A . 8.5% B . 9% C . 9.5% D . 10%

答案解析收藏纠错 + 选题
15. 如图是一块矩形菜地ABCD，AB=am，AD=bm，面积为Sm² ，现将边AB增加1m．
1. （1）如图①，若a=5，边AD减少1 m，得到的矩形面积不变，则b的值是.
2. （2）如图②，若边AD增加2 m，有且只有一个a的值，使得到的矩形面积为2S m² ，则S的值是.
答案解析收藏纠错 + 选题
16. (2024八下·浙江期中) 古巴比伦挖掘出的泥版中，记载着一元二次方程正数解的几何解法．以 $\text{[math]}$ 为例说明，如图1，构造一个边长为x的正方形，加上一个长为x宽为10的长方形；再将右边的长方形剪成2个宽为5的长方形，拼成边长为 $\text{[math]}$ 的大正方形，如图2所示，则大正方形的面积为 $\text{[math]}$ ，即可求得 $\text{[math]}$ ．小明用此几何法解关于x的方程 $\text{[math]}$ ，若假设图1中正方形的面积为81，图2中大正方形的面积为144，则 $\text{[math]}$ ， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2024·绵阳模拟) 有一人利用手机发短信，获得他信息的人也按他的发送人数发送该条短信，经历两轮短信的发送，共有110人的手机获得该条短信．设每人给y人发短信，则可列方程．

答案解析收藏纠错 + 选题

18. (2024八下·义乌期中) 根据以下素材，探索完成任务．

素材1	某校统一安装了日光灯，日光灯中最易损坏的是灯管和镇流器．
素材2	该校后勤部准备补进灯管和镇流器共400件．批发市场灯管的单价为30元，镇流器的单价为80元．商家为了促销且保证有一定的利润，当镇流器购买数量超过80件时，每多购买1件，单价下降1元，但单价不低于50元．
问题解决
任务1	若镇流器补进90件，则学校补进镇流器和灯管共多少元？
任务2	设镇流器补进x件，若 $\text{[math]}$ ，刚补进镇流器的单价为 ▲ 元，补进灯管的总价为 ▲ （用含x的代数式表示）；
任务3	若学校后勤部补进镇流器和灯管共花15000元，求补进镇流器多少件？

答案解析收藏纠错 + 选题

19. (2024八下·杭州期中) 根据以下销售情况，解决销售任务．

	销售情况分析
	总公司将一批衬衫由甲、乙两家分店共同销售，因地段不同，它们的销售情况如下：
店面	甲店	乙店
日销售情况	每天可售出20件，每件盈利40元．	每天可售出32件，每件盈利30元．
市场调查	经调查发现，每件衬衫每降价1元，甲、乙两家店一天都可多售出2件．
情况设置	设甲店每件衬衫降价 $\text{[math]}$ 元，乙店每件衬衫降价 $\text{[math]}$ 元．

（1）【任务1】甲店每天的销售量（用含 $\text{[math]}$ 的代数式表示）．
乙店每天的销售量（用含 $\text{[math]}$ 的代数式表示）．
（2）【任务2】当 $\text{[math]}$ ， $\text{[math]}$ 时，分别求出甲、乙店每天的盈利．
（3）【任务3】总公司规定两家分店下降的价格必须相同，请求出每件衬衫下降多少元时，两家分店一天的盈利和为2244元．

答案解析收藏纠错 + 选题

20. (2024八下·北仑期中) 根据以下素材，完成探索任务．

探索果园土地规划和销售利润问题
素材1	某农户承包了一块长方形果园
	ABCD ，图1是果园的平面图，其中AB＝
	200米，BC＝300米．准备在它的四周铺
	设道路，上下两条横向道路的宽度都为2x
	米，左右两条纵向道路的宽度都为x米，
	中间部分种植水果．
	出于货车通行等因素的考虑，道路宽
	度x不超过12米，且不小于5米．
素材2	该农户发现某一种草莓销售前景比较
	不错，经市场调查，草莓培育一年可产
	果，若每平方米的草莓销售平均利润为
	100元，每月可销售5000平方米的草莓；
	受天气原因，农户为了快速将草莓出手，
	决定降价，若每平方米草莓平均利润下调
	5元，每月可多销售500平方米草莓.果园
	每月的承包费为2万元.
问题解决
任务1	解决果园中路面宽度的设计对种植面	（1）请直接写出纵向道路宽度x的取
	积的影响．	值范围．
		（2）若中间种植的面积是44800m2，
		则路面设置的宽度是否符合要求．
任务2	解决果园种植的预期利润问题．	（3）若农户预期一个月的总利润为52
	（总利润=销售利润-承包费）	万元，则从购买草莓客户的角度应该降
	（总利润=销售利润-承包费）	价多少元？

答案解析收藏纠错 + 选题

21. (2023八下·上城期末) 综合实践：

项目主题	“亚运主题”草坪设计
项目情境	为了迎亚会，同学们参与一块长为40米，宽为30米的矩形“亚运主题”草坪方案设计的项目学习．以下为项目学习小组对草坪设计的研究过程．
活动任务一	请设计两条相同宽度的小路连接矩形草坪两组对边．小组内同学们设计的方案主要有甲、乙、丙、丁四种典型的方案
驱动问题一	（1）项目小组设计出来的四种方案小路面积的大小关糸？ ①直观猜想：我认为 ▲ ；（请用简洁的语言或代数式表达你的猜想） ②具体验证：选择最简单的甲、乙方案，假设小路宽为1米，则甲、乙方案中小路的面积分别为 ▲ 和 ▲ ； ③一般验证：若小路宽为x米，则甲、乙方案中小路所占的面积分别为 ▲ 和 ▲ ．
活动任务二	为施工方便，学校选择甲种方案设计，并要求除小路后草坪面积约为1064平方米．
驱动问题二	（2）请计算两条小路的宽度是多少？
活动任务三	为了布置五环标志等亚运元素，将在草坪上的亚运宣传主题墙前，用篱笆围（三边）成面积为100平方米的矩形 $\text{[math]}$ ，如图．
驱动问题三	（3）为了使篱笆恰好用完同时围住三面，项目小组的同学对下列问题展开探究，其中矩形宽 $\text{[math]}$ ，长 $\text{[math]}$ ． ①若30米长的篱笆，请用两种不同的函数表示y关于x的函数关系． ②数学之星小明提出一个问题：若a米长的篱笆恰好用完，且有两种不同方案可以选择，使得两种方案的宽之和小于15米，甲同学说“篱笆的长可以是28米”，乙同学说“篱笆的长可以是32米”，你认为他们俩的说法对吗？请说明理由．

答案解析收藏纠错 + 选题

22. (2024八下·温州期中) 综合与实践：

如何改造儿童友好公园？
素材1	在一块长与宽之比为 $\text{[math]}$ 的长方形场地 $\text{[math]}$ 上，有两条宽度都为4米的通道（阴影部分）栽种花草（如图1）．剩余空地面积为场地 $\text{[math]}$ 面积的一半．
素材2	为了在该场地安装大型儿童游乐设施，需将场地改造为图2方案．已知 $\text{[math]}$ 米， $\text{[math]}$ 米，阴影部分区域栽种花草，长方形空地 $\text{[math]}$ 安装游乐设施．
问题解决
目标1	确定场地尺寸	求长方形 $\text{[math]}$ 的长和宽．
目标2	确定改造方案1	若剩余空地面积为场地 $\text{[math]}$ 面积的 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为正整数，请你设计一种方案： $\text{[math]}$ ________米， $\text{[math]}$ ________米．
目标2	确定改造方案2	若 $\text{[math]}$ 比 $\text{[math]}$ 大8米，求长方形空地 $\text{[math]}$ 面积的最大值．

答案解析收藏纠错 + 选题

三、数据分析初步

23. (2024八下·鄞州期中) 某班级采用小组学习制，在一次数学单元测试中，第一组成员的测试成绩分别为：96，90，100，80，96，其中得分80的同学有一道题目被老师误判，其实际得分应该为90分，那么该小组的实际成绩与之前成绩相比，下列说法正确的是（）

A . 数据的平均数不变 B . 数据的众数不变 C . 数据的中位数不变 D . 数据的方差不变

答案解析收藏纠错 + 选题
24. (2024八下·绍兴期中) 在一次素养比赛中，6位学生的成绩分别为65分，65分，80分，85分，90分，90分，统计时误将一位学生的成绩65分记成了60分，则其中不受影响的统计量是（）

A . 平均数 B . 中位数 C . 众数 D . 方差

答案解析收藏纠错 + 选题
25. (2024八下·余杭期中) 水果店里有一批大小不一的西瓜，餐厅经理选择了部分大小均匀的西瓜．设水果店里的西瓜的质量（单位：kg）平均数和方差分别为 $\text{[math]}$ ， $\text{[math]}$ ，餐厅经理选购的西瓜的质量的平均数和方差分别为 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论一定成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

26. (2024八下·鄞州期中) 下表记录了四位射击运动员选拔比赛成绩的平均数和方差：

运动员	甲	乙	丙	丁
平均数（环）	9.1	9.2	9.1	9.2
方差（环 $\text{[math]}$ ）	3.5	15.5	16.5	3.5

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题

27. (2024八下·吴兴期中) 某校规定：学生的单科学期综合成绩是由平时、期中和期末三项成绩按2：3：5的比例计算所得．已知某学生本学期数学的平时、期中和期末成绩分别是85分、90分和96分，那么他本学期数学学期综合成绩是分．

答案解析收藏纠错 + 选题
28. (2024八下·北仑期中) 为弘扬传统文化，某校在读书节举行了“诗词竞赛”，某班20名同学参加了此次竞赛，他们的得分情况如下表所示，则全班20名同学的成绩的中位数是．
人数
2
7
7
4
成绩（分）
70
80
90
100

答案解析收藏纠错 + 选题
29. (2024九下·广西壮族自治区模拟) 小明某学期的数学平时成绩 $\text{[math]}$ 分，期中考试 $\text{[math]}$ 分，期末考试 $\text{[math]}$ 分，若计算学期总评成绩的方法如下，平时：期中：期末 $\text{[math]}$ ，则小明学期总评成绩是分．

答案解析收藏纠错 + 选题
30. (2024八下·鄞州期中) 为了开展阳光体育运动，提高学生身体素质，学校开设了“引体向上”课程．为了解学生做引体向上的情况，现从八年级各班随机抽取了部分男生进行测试，绘制出不完整的统计图1和图2，请根据有关信息，解答下列问题：
1. （1）本次接受随机抽样调查的男生人数为，图1中m的值是；
2. （2）本次调查获取的样本数据（6，7，8，9，10）中，众数为，中位数为；
3. （3）补全条形统计图；
4. （4）根据样本数据，若八年级有280名男生，请你估计该校八年级男“引体向上”次数在8次及以上的人数．
答案解析收藏纠错 + 选题
31. (2024八下·义乌月考) 综合与实践
【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动，
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如下：

1
2
3
4
5
6
7
8
9
10
芒果树叶的长宽比
3.8
3.7
3.5
3.4
3.8
4.0
3.6
4.0
3.6
4.0
荔枝树叶的长宽比
2.0
2.0
2.0
2.4
1.8
1.9
1.8
2.0
1.3
1.9
【实践探究】分析数据如下：

平均数
中位数
众数
方差
芒果树叶的长宽比
3.74
m
4.0
0.0424
荔枝树叶的长宽比
1.91
2.0
n
0.0669
问题解决】
1. （1）上述表格中， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2） ①A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大．”
  ②B同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍．”
  上面两位同学的说法中，合理的是（填序号）
3. （3）现有一片长 $\text{[math]}$ ，宽 $\text{[math]}$ 的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由．
答案解析收藏纠错 + 选题
32. (2023八下·杭州期末) 某班开展一次综合与实践活动，部分记载如下：
【活动主题】利用树叶的特征对树木进行分类．
【实践过程】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如表：

1
2
3
4
5
6
7
8
9
10
芒果树叶的长宽比
3.8
3.7
3.5
3.4
3.8
4.0
3.6
4.0
3.6
4.0
荔枝树叶的长宽比
2.0
2.0
2.0
2.4
1.8
1.9
1.8
2.0
1.3
1.9
【问题解决】
1. （1）同学们通过计算得到芒果树叶的长宽比的平均数是3.74，请你继续计算出荔枝树叶的长宽比的平均数；
2. （2）从树叶的长宽比的平均数来看，现有一片长13cm，宽6.5cm的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树？并给出你的理由．
答案解析收藏纠错 + 选题

33. (2023八下·嘉兴期末) 某校文化艺术节举办班级赛歌活动，分为初赛和决赛．

（1）初赛阶段，8个评委给某班的打分情况如下（单位：分）．
评委1
评委2
评委3
评委4
评委5
评委6
评委7
评委8
9.5
9.4
9.4
9.5
9.5
9.3
9.3
9.6
写出这组数据的中位数和众数；

（2）决赛阶段，801班和803班角逐冠亚军，评委分别从表现形式、情感演绎、音色音准三个方面打分，得分如右表所示（单位：分）．学校将表现形式、情感演绎、音色音准以2：3：5的比例确定最终得分，请你通过计算说明哪个班级获得冠军．

班级	表现形式	情感演绎	音色音准
801	9.5	9.6	9.5
803	9.4	9.8	9.4

答案解析收藏纠错 + 选题

34. (2023八下·滨江期末) 称五筐大白菜的重量，得到如下统计表中甲组数据．把甲组数据的每个数都减去 $\text{[math]}$ ，得到统计表中的乙组数据，将这两组数据分别画成折线统计图（未完成．单位：千克）．

甲组、乙组数据统计表

序号	1	2	3	4	5
甲组数据	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
乙组数据	$\text{[math]}$	2	$\text{[math]}$	$\text{[math]}$	3

请完成下列问题：

（1）完成乙组数据的折线统计图．
（2） ①分别求出甲、乙两组数据的平均数 $\text{[math]}$ ， $\text{[math]}$ ，并直接写出 $\text{[math]}$ 与 $\text{[math]}$ 之间满足的数量关系式．
②甲、乙两组数据的方差分别为 $\text{[math]}$ ， $\text{[math]}$ ，请比较 $\text{[math]}$ ， $\text{[math]}$ 的大小，并说明理由．

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

命题新趋势3 真实情境（1）——2024年浙教版数学八（下）...

副标题：

*注意事项：

命题新趋势3 真实情境（1）——2024年浙教版数学八（下）...

试题分析

总体分析

题量分析

难度分析

知识点分析

	1	2	3	4	5	6	7	8	9	10
芒果树叶的长宽比	3.8	3.7	3.5	3.4	3.8	4.0	3.6	4.0	3.6	4.0
荔枝树叶的长宽比	2.0	2.0	2.0	2.4	1.8	1.9	1.8	2.0	1.3	1.9

	平均数	中位数	众数	方差
芒果树叶的长宽比	3.74	m	4.0	0.0424
荔枝树叶的长宽比	1.91	2.0	n	0.0669

评委1	评委2	评委3	评委4	评委5	评委6	评委7	评委8
9.5	9.4	9.4	9.5	9.5	9.3	9.3	9.6

人数	2	7	7	4
成绩（分）	70	80	90	100