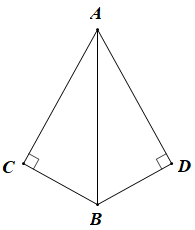
 B .
B .  C .
C .  D .
D . 



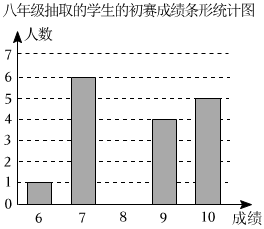
七、八年级抽取的学生的初赛成绩统计表:
|
年级 |
七年级 |
八年级 |
|
平均数 |
|
|
|
中位数 |
|
|
|
众数 |
|


若梯子底端位置保持不动,将梯子斜靠在右墙时,梯子顶端距离地面的距离为1.5m,求小巷有多宽?
