


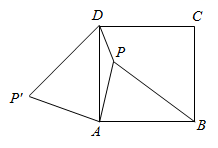
① 可以由
绕点A逆时针旋转
得到;②点P与
的距离为2;③
;④
;⑤
.其中正确的结论是(填序号).


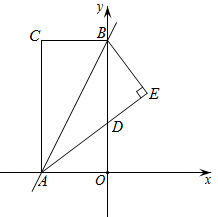
①求证:.
②若 ,
, 求AH的长.
从正方形的一个顶点引出夹角为 如图1,在正方形 大致证明思路:如图2,将 |
任务:

如图3,在四边形中,
,
,
, 以
为顶点的
,
、
与
、
边分别交于
、
两点.请参照阅读材料中的解题方法,你认为结论
是否依然成立,若成立,请写出证明过程;若不成立,请说明理由.