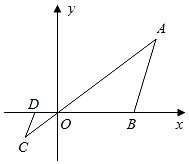

①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
其中正确命题的序号是( )
 B .
B .  C .
C . 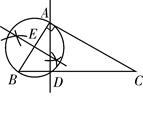 D .
D . 


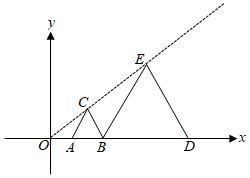
制作:把钻有若干等距小孔的四根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点, ,
, 在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
原理:
连接 ,
, 可证得以下结论:
①和
为等腰三角形,则
,
(180°-∠ ▲ );
②四边形为平行四边形(理由是 ▲ );
③ , 于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的 ▲ 倍得到的.
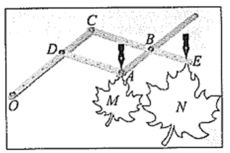
制作:把钻有若干等距小孔的四根直尺用螺栓分别在点 ,
,
,
处连接起来,使得直尺可以绕着这些点转动,
为固定点,
,
,在点
,
处分别装上画笔.
画图:现有一图形 ,画图时固定点
,控制点
处的笔尖沿图形
的轮廓线移动,此时点
处的画笔便画出了将图形
放大后的图形
.
原理:
连接 ,
,可证得以下结论:
① 和
为等腰三角形,则
,
(180°-∠ ▲ );
②四边形 为平行四边形(理由是 ▲ );
③ ,于是可得
,
,
三点在一条直线上;
④当 时,图形
是以点
为位似中心,把图形
放大为原来的 ▲ 倍得到的.

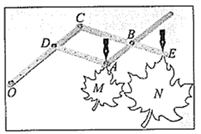
用硬纸板复制视力表中所对应的“E”,并依次编号为①,②,放在水平桌面上.如图所示,将②号“E”沿水平桌面向右移动,直至从观测点O看去,对应顶点 ,
, O在一条直线上为止.这时我们说,在
处用①号“E”测得的视力与在
处用②号“E”测得的视力相同.

解决问题
小明观察一个由1×1正方形点阵组成的点阵图,图中水平与竖直方向上任意两个相邻点间的距离都是1.他发现一个有趣的问题:对于图中出现的任意两条端点在点阵上且互相不垂直的线段,都可以在点阵中找到一点构造垂直,进而求出交点与垂足之间的数值.

请回答:
请你帮小明计算:OC=OF=;
如图3,线段AB与CD交于点O . 在点阵中找到点E , 连接AE , 满足AE⊥CD于F . 计算: OC=,OF=.