
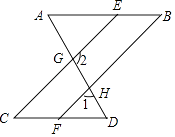
已知:如图,已知 ,
,
,
求证:.

证明:∵.
∴ ▲ ( ),
∵ , ∴
▲ ,
即 , ∴
,
∵ , ∴
▲ ( ),
∴ ▲ ( ),
又∵ ,
∴( ).




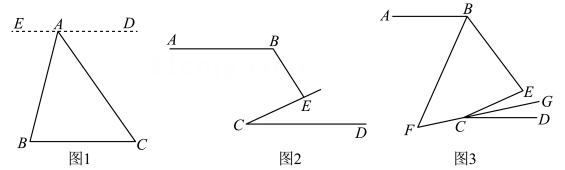
如图1,已知点A是BC外一点,连接AB,AC.求的度数.
解:过点作
,
,
,
又.
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将“凑”在一起,得出角之间的关系,使问题得以解决.

解:过点A作 ,

▲ ,
▲ ,
,
.
①如图3,点B在点A的左侧,若 , 求
的度数.
②如图4,点B在点A的右侧,且 ,
.若
, 求
度数.(用含n的代数式表示)