
通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
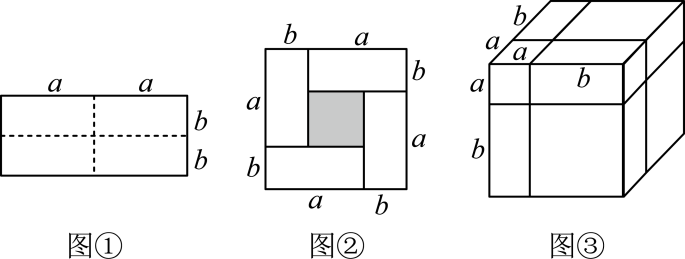
例如:如图①是个长为 , 宽为
的长方形,沿图中虚线用剪刀将其均分成四个小长方形,然后按如图②的形状拼成一个正方形.请解答下列问题:
方法1:;方法2:;
由此可以得出之间的等量关系是;
类似地,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
如图③,请用两种不同的方法表示这个几何体的体积,并写出一个恒等式;
①化简:(a-b)(a2+ab+b2)=;
②计算:(993+1)÷(992-99+1)=;
数形结合思想是根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的思想.我们常利用数形结合思想,借助形的几何直观性来阐明数之间某种关系,如:探索整式乘法的一些法则和公式.
探索整式乘法的一些法则和公式.

在大正方体一角截去一个棱长为b(b<a)的小正方体,如图3所示,则得到的几何体的体积为 ;

杨辉,南宋杰出的数学家和数学教育家,杨辉一生留下了大量的著作,他著名的数学著作共5种21卷,即《详解九章算法》12卷,《日用算法》2卷,《乘除通变本末》3卷,《田亩比类乘除捷法》卷,《续古摘奇算法》卷。在《详解九章算法》一书中,画了一张表示二项式展开后的系数构成的三角图形,根据这个三角图形,杨辉研究了二项式定理,并根据此定理研究了两教的立方和、立方差、三数的立方和等公式,两数的立方差公式是:a3-b3=(a-b)(a2+ab+b2),这个公式的推导过程如下:a3-b3=a3-a2b+a2b-b3=a2(a-b)+b(a2-b2)=a2(a-b)+b(a+b)(a-b)=(a-b)(a2+ab+b2)
任务:
杨辉三角如果将
将上述每个式子的各项系数排成该表.
观察该表,可以发现每一行的首末都是1,并且下一行的数比上一行多1个,中间各数都写在上一行两数的中间,且等于它们的和.按照这个规律可以将这个表继续往下写. 该表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过,而他是摘录自北宋时期数学家贾宪著的《开方作法本源》中的“开方作法本源图",因而人们把这个表叫做杨辉三角或贾宪三角,在欧洲这个表叫做帕斯卡三角形.帕斯卡(B.Pascal,1623—1662)是1654年发现这一规律的,比杨辉要迟393年,比贾宪迟600年. |
②的展开式中共有项,所有项的系数和为;
杨辉三角是我国南宋数学家杨辉发现的,利用杨辉三角可以很方便地写出两项多项式的 次方的展开式.杨辉三角中的每一行的数分别对应两项多项式
次方展开式中的各项系数.例如:
,右边的系数1、2、1是杨辉三角中第三行的三个数,又如:
中右边各项系数1、3、3、1是杨辉三角中第四行的四个数.根据这个规律,试解决下列问题:

(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=(a+b)(a2+2ab+b2)=a3+3a2b+3ab2+b3
(a+b)4=(a+b)(a3+3a2b+3ab2+b3)=a4+4a3b+6a2b2+4ab3+b4
“杨辉三角”里面蕴藏了许多的规律