①当 ,
两点之间的距离为2时,求的值.
②同一时间,动点从点
出发,以每秒4个单位长度的速度沿数轴向右匀速运动,当
,
两点相遇时,求点
在数轴上所表示的数.
数学课上,老师给出了如下问题:
如图1, ,
平分
, 若
, 请你补全图形,并求
的度数.
小明做题时画出了如图2的图形,小静说“我觉得这个题有两种情况,小明考虑的是在
外部的情况,事实上,
还可能在
的内部”.

请你完成以下问题:
对称式: 一个含有多个字母的式子中,任意交换两个字母的位置,当字母的取值均不相等,且都不为 |
问题:
写出一个只含有字母
,
的三次三项式,使该多项式是对称式;
【阅读材料】我们知道: , 类似地,我们把
看成一个整体,则
. “整体思想”是数学的一种重要思想,它在多项式的化简与求值中应用极为广泛.
求的值.
角是一种基本的几何图形,如图1角可以看作由一条射线绕着它的端点旋转而形成的图形,钟面上的时针与分针给我们以角的形象,如果把图2作为钟表的起始状态,对于一个任意时刻时针与分针的夹角度数可以用下面的方法确定.

因为时针绕钟面转一圈(360°)需要12小时,所以时针每小时转过30°.
因为分针绕钟面转一圈(360°)需要60分钟,所以分针每分钟转过6°.
例如:05:40时针转过的度数为 , 分针转过的度数为
, 此时,分针转过的度数大于时针转过的度数,所以05:40时针与分针的夹角为
.
请使用上述方法,求出03:20时针与分针的夹角.
03:00后再经过 , 钟表的分针与时针重合,求x的值.
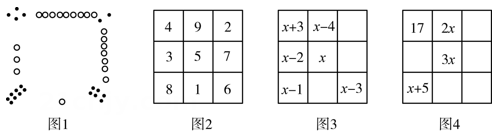
“九宫图”源于我国古代夏禹时期的“洛书”(如图1),是世界上最早的矩阵,又称幻方.用今天的数学符号表示,洛书就是一个三阶幻方(如图2),“幻方”需要满足的条件是每一行、每一列和每条对角线上各个数之和都相等.

阅读材料,解答下列问题:
幻方历史悠久,传说最早出现在夏禹时代的“洛书”,如图1.把图1的洛书用今天的数学符号翻译出来,就是一个三阶幻方,如图2,它的每行、每列、每条对角线上的三个数的和都相等. |
【方法迁移】
如图2,平分
.现有射线OP、OQ分别从OC、OB同时出发,以每秒
和每秒
的速度绕点
顺时针旋转,当OP旋转一周时,这两条射线都停止旋转.问经过几秒后,射线OP、OQ的夹角为
【生活运用】
周末的下午,小明看到钟面显示3点整,此时分针与时针的夹角恰好为 , 经过多少分钟后,分针与时针的夹角首次变成

已知是关于x的二次二项式,A,B是如图1数轴上两点,且A,B对应的数分别为a,b.C是线段
的中点.
①A点对应的数 ▲ , B点对应的数
▲ , 点C表示的数是 ▲ ;
②若点P、Q分别从点C、B同时出发,以每秒3个单位长度和1个单位长度的速度沿数轴正方向运动,则t秒后,点P、Q表示的数分别是 ▲ 、 ▲ (用含t的代数式表示);
③在(2)的条件下,若P、O两点之间的距离为2.求t的值.
如图2, ,
平分
. 现有射线
、
分别从
、
同时出发,以每秒
和每秒
的速度绕点O顺时针旋转,当
旋转一周时,这两条射线都停止旋转,问经过几秒后,射线
、
的夹角为
?
周末的下午,小明看到钟面显示3点整,此时分针与时针的夹角恰好为 , 经过多少分钟后,分针与时针的夹角首次变成
?
【阅读】幻方历史悠久,传说最早出现在夏禹时代的“洛书”如图
, 把洛书用今天的数学符号翻译出来就是图
的三阶幻方,它的每行、每列、每条对角线上的三个数的和都为
.

【问题背景】数轴是一个非常重要的数学工具,使数和数轴上的点建立起对应关系,这样能够用“数形结合”的方法解决一些实际问题.如图,在纸面上有一数轴,按要求折叠纸面:
![]()
【问题解决】
(1)若折叠后数1对应的点与数对应的点重合,则此时数
对应的点与数________对应的点重合;
【学以致用】
(2)若折叠后数2对应的点与数对应的点重合,则此时数0对应的点与数________对应的点重合;
【问题拓展】
(3)若如(2)这样折叠后,数轴上有A、B两点也重合,且A、B两点之间的距离为11(点B在A点的右侧),则点A对应的数为________,点B对应的数为________;
(4)在(3)的条件下,数轴上有一动点P,动点P从B点出发,以每秒2个单位长度的速度在数轴上匀速运动,设运动时间为t秒().
①动点P从B点向右出发,t为何值时,P、A两点之间的距离为15个单位长度;
②请直接写出动点P从B点向左出发时,P、A两点之间的距离为15个单位长度的t的值.