人教版数学八年级下学期勾股定理单元试卷

更新时间：2018-02-24 浏览次数：1089 类型：单元试卷

一、单选题

1. (2017九上·东台月考) 如图，半圆O的直径AB=10cm，弦AC=6cm，AD平分∠BAC，则AD长（）

A . 4 $\text{[math]}$ cm B . 3 $\text{[math]}$ cm C . 5 $\text{[math]}$ cm D . 4 cm

答案解析收藏纠错 + 选题
2. (2016九下·萧山开学考) 如图，在△ABC中，BC=10，∠B=60°，∠C=45°，则点A到BC的距离是（）

A . 10﹣5 $\text{[math]}$ B . 5+5 $\text{[math]}$ C . 15﹣5 $\text{[math]}$ D . 15﹣10 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021八上·滕州月考) 如图，在矩形ABCD中，BC=6，CD=3，将△BCD沿对角线BD翻折，点C落在点C′处，BC′交AD于点E，则线段DE的长为（）.

A . 3 B . $\text{[math]}$ C . 5 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022八下·重庆月考) 如图，在矩形ABCD中，AB=4，AD=6，点F是AB的中点，E为BC边上一点，且EF⊥ED，连结DF，M为DF的中点，连结MA，ME．若AM⊥ME，则AE的长为（）

A . 5 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2017九上·南山月考) 如图，已知正方形ABCD的边长为2，E是边BC上的动点，BF⊥AE交CD于点F，垂足为点G，连接CG，下列说法：①AG＞GE；②AE=BF；③点G运动的路径长为π；④CG的最小值 $\text{[math]}$ ﹣1．其中正确的说法有（）个．

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
6. (2017·宁波)
如图，四边形ABCD是边长为6的正方形，点E在边AB上，BE＝4，过点E作EF∥BC，分别交BD、CD于G、F两点．若M、N分别是DG、CE的中点，则MN的长为（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
7. (2017·黄石) 如图，△ABC中，E为BC边的中点，CD⊥AB，AB=2，AC=1，DE= $\text{[math]}$ ，则∠CDE+∠ACD=（）

A . 60° B . 75° C . 90° D . 105°

答案解析收藏纠错 + 选题
8. (2017·温州)
四个全等的直角三角形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为S的小正方形EFGH．已知AM为Rt△ABM较长直角边，AM=2 $\text{[math]}$ EF，则正方形ABCD的面积为（）

A . 12S B . 10S C . 9S D . 8S

答案解析收藏纠错 + 选题
9. (2021八上·滕州月考) 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F．若AC=3，AB=5，则CE的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、综合题

10. (2017九上·东台月考) 如图，A（-5，0），B（-3，0），点C在y轴的正半轴上，∠CBO=45°，CD∥AB．∠CDA=90°．点P从点Q（4，0）出发，沿x轴向左以每秒1个单位长度的速度运动，运动时时间t秒．
1. （1）求点C的坐标；
2. （2）当∠BCP=15°时，求t的值；
3. （3）以点P为圆心，PC为半径的⊙P随点P的运动而变化，当⊙P与四边形ABCD的边（或边所在的直线）相切时，求t的值．
答案解析收藏纠错 + 选题
11. (2016九下·澧县开学考) 在图1﹣﹣图4中，菱形ABCD的边长为3，∠A=60°，点M是AD边上一点，且DM= $\text{[math]}$ AD，点N是折线AB﹣BC上的一个动点．
1. （1）如图1，当N在BC边上，且MN过对角线AC与BD的交点时，则线段AN的长度为．
2. （2）当点N在AB边上时，将△AMN沿MN翻折得到△A′MN，如图2，
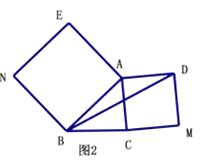
  ①若点A′落在AB边上，则线段AN的长度为；
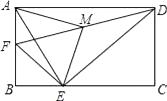
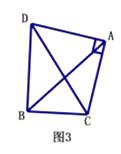
  ②当点A′落在对角线AC上时，如图3，求证：四边形AM A′N是菱形；
  ③当点A′落在对角线BD上时，如图4，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
12. (2017九上·南山月考) 根据所学知识完成小题：
1. （1）如图1，锐角△ABC中，分别以AB、AC为边向外作等边△ABE和等边△ACD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．
2. （2）【深入探究】如图2，△ABC中，∠ABC=45°，AB=5cm，BC=3cm，分别以AB、AC为边向外作正方形ABNE和正方形ACMD，连接BD，求BD的长．
3. （3）如图3，在（2）的条件下，以AC为直角边在线段AC的左侧作等腰直角△ACD，求BD的长．
答案解析收藏纠错 + 选题
13. (2017·盐城模拟) 在四边形ABCD中，AB∥CD，∠BCD=90°，AB=AD=10cm，BC=8cm，点P从点A出发，沿折线ABCD方向以3cm/s的速度匀速运动；点Q从点D出发，沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发，当一个点到达终点时，另一点也停止运动，设运动时间为t（s）.
1. （1）求CD的长；
2. （2）当四边形PBQD为平行四边形时，求四边形PBQD的周长；
3. （3）在点P、Q的运动过程中，是否存在某一时刻，使得△BPQ的面积为20cm²？若存在，请求出所有满足条件的t的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题
14. (2017·河源模拟) 如图，D是△ABC的边AB上一点，CN∥AB，DN交AC于点M，若MA=MC．
1. （1）求证：CD=AN；
2. （2）若AC⊥DN，∠CAN=30°，MN=1，求四边形ADCN的面积．
答案解析收藏纠错 + 选题
15. (2017·兰州模拟) 如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC且DE= $\text{[math]}$ AC，连接AE交OD于点F，连接CE、OE．
1. （1）求证：OE=CD；
2. （2）若菱形ABCD的边长为2，∠ABC=60°，求AE的长．
答案解析收藏纠错 + 选题
16. (2021九上·昆都仑月考) 如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立．
1. （1）当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．
2. （2）当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G．
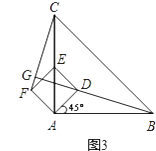
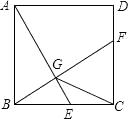
  ①求证：BD⊥CF；
  ②当AB=4，AD= $\text{[math]}$ 时，求线段BG的长．
答案解析收藏纠错 + 选题
17. (2021八下·越秀期中)
如图，在正方形ABCD中，点G在对角线BD上（不与点B，D重合），GE⊥DC于点E，GF⊥BC于点F，连结AG．
1. （1）写出线段AG，GE，GF长度之间的数量关系，并说明理由；
2. （2）若正方形ABCD的边长为1，∠AGF=105°，求线段BG的长．
答案解析收藏纠错 + 选题
18. (2019八下·宽城期末)
如图，在△ABC中，点O是边AC上一个动点，过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F．
1. （1）若CE=8，CF=6，求OC的长；
2. （2）
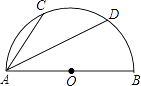
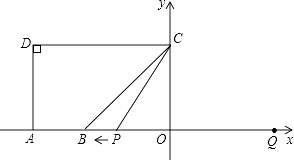
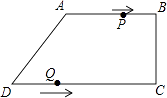
  连接AE、AF．问：当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．
答案解析收藏纠错 + 选题
19. (2017·扬州) 我们规定：三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差．如图1，在△ABC中，AO是BC边上的中线，AB与AC的“极化值”就等于AO²﹣BO²的值，可记为AB△AC=AO²﹣BO² ．
1. （1）
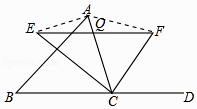
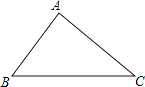
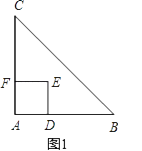
  在图1中，若∠BAC=90°，AB=8，AC=6，AO是BC边上的中线，则AB△AC=，OC△OA=；
2. （2）
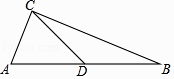
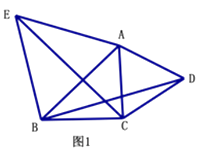
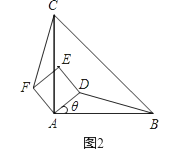
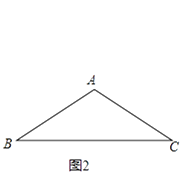
  如图2，在△ABC中，AB=AC=4，∠BAC=120°，求AB△AC、BA△BC的值；
3. （3）
  如图3，在△ABC中，AB=AC，AO是BC边上的中线，点N在AO上，且ON= $\text{[math]}$ AO．已知AB△AC=14，BN△BA=10，求△ABC的面积．
答案解析收藏纠错 + 选题
20. (2017·东营)
如图，在等腰三角形ABC中，∠BAC=120°，AB=AC=2，点D是BC边上的一个动点（不与B、C重合），在AC上取一点E，使∠ADE=30°．
1. （1）求证：△ABD∽△DCE；
2. （2）设BD=x，AE=y，求y关于x的函数关系式并写出自变量x的取值范围；
3. （3）当△ADE是等腰三角形时，求AE的长．
答案解析收藏纠错 + 选题
21. (2017·广州)
如图，矩形ABCD的对角线AC，BD相交于点O，△COD关于CD的对称图形为△CED．
1. （1）求证：四边形OCED是菱形；
2. （2）连接AE，若AB=6cm，BC= $\text{[math]}$ cm．
  ①求sin∠EAD的值；
  ②若点P为线段AE上一动点（不与点A重合），连接OP，一动点Q从点O出发，以1cm/s的速度沿线段OP匀速运动到点P，再以1.5cm/s的速度沿线段PA匀速运动到点A，到达点A后停止运动，当点Q沿上述路线运动到点A所需要的时间最短时，求AP的长和点Q走完全程所需的时间．
答案解析收藏纠错 + 选题

三、填空题

22. (2024九上·沭阳期末) 一等腰三角形的两边长分别为4cm和6cm，则其底角的余弦值为．

答案解析收藏纠错 + 选题
23. (2021·邵武模拟)
如图，在菱形纸片ABCD中，AB＝2，∠A＝60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F、G分别在边AB、AD上．则cos∠EFG的值为．

答案解析收藏纠错 + 选题
24. (2021八下·官渡期末) 如图，△ABC中，AC=5，BC=12，AB=13，CD是AB边上的中线．则CD=．

答案解析收藏纠错 + 选题
25. (2021·梁山模拟)
如图，在Rt△ABC中，∠BAC=90°，AB=15，AC=20，点D在边AC上，AD=5，DE⊥BC于点E，连结AE，则△ABE的面积等于．

答案解析收藏纠错 + 选题
26. (2021八下·玉泉期中)
如图，已知菱形ABCD的周长为16，面积为8 $\text{[math]}$ ，E为AB的中点，若P为对角线BD上一动点，则EP+AP的最小值为．

答案解析收藏纠错 + 选题
27. (2017·襄阳) 如图，在△ABC中，∠ACB=90°，点D，E分别在AC，BC上，且∠CDE=∠B，将△CDE沿DE折叠，点C恰好落在AB边上的点F处．若AC=8，AB=10，则CD的长为．

答案解析收藏纠错 + 选题
28. (2017·咸宁)
如图，在Rt△ABC中，BC=2，∠BAC=30°，斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动，下列结论：
①若C、O两点关于AB对称，则OA=2 $\text{[math]}$ ；
②C、O两点距离的最大值为4；
③若AB平分CO，则AB⊥CO；
④斜边AB的中点D运动路径的长为 $\text{[math]}$ ；
其中正确的是（把你认为正确结论的序号都填上）．

答案解析收藏纠错 + 选题
29. (2017·广州)
如图，平面直角坐标系中O是原点，▱ABCD的顶点A，C的坐标分别是（8，0），（3，4），点D，E把线段OB三等分，延长CD、CE分别交OA、AB于点F，G，连接FG．则下列结论：
①F是OA的中点；②△OFD与△BEG相似；③四边形DEGF的面积是 $\text{[math]}$ ；④OD= $\text{[math]}$
其中正确的结论是（填写所有正确结论的序号）．

答案解析收藏纠错 + 选题

四、解答题

30. (2017·宁波)
在一次课题学习中，老师让同学们合作编题．某学习小组受赵爽弦图的启发，编写了下面这道题，请你来解一解．
如图，将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H，使得AE＝CG，BF＝DH，连结EF、FG、GH、HE．
1. （1）求证：四边形EFGH为平行四边形；
2. （2）若矩形ABCD是边长为1的正方形，且∠FEB＝45°，tan∠AEH＝2，求AE的长．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

人教版数学八年级下学期勾股定理单元试卷

副标题：

*注意事项：

人教版数学八年级下学期勾股定理单元试卷

试题分析

总体分析

题量分析

难度分析

知识点分析