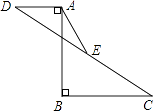
①OA=OD;
②AD⊥EF;
③AE+DF=AF+DE;
④当∠BAC=90°时,四边形AEDF是正方形.
其中一定正确的是( )
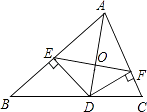
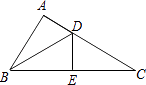
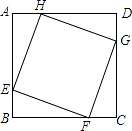
如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:
①△ABM≌△DCN;②∠DAF=30°;③△AEF是等腰直角三角形;④EC=CF;⑤S△HCF=S△ADH ,
其中正确的结论有( )
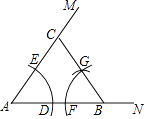
以点A为圆心,以任意长为半径作弧,交AN于点D,交AM于点E;以点B为圆心,以AD为半径作弧,交AB于点F;以点F为圆心,以DE为半径作弧,交前面的弧于点G;连接BG并延长交AM于点C.则∠BCM的度数为( )
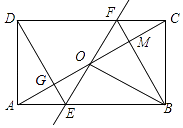
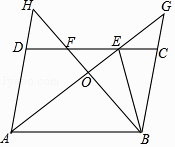
如图,在▱ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
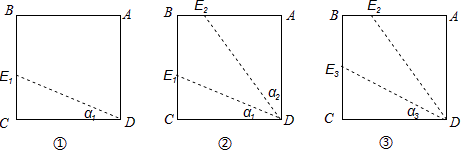
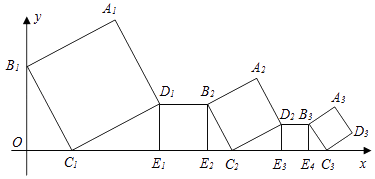
(i)过点D任作一条直线与BC边相交于点E1(如图①),记∠CDE1=α1;
(ii)作∠ADE1的平分线交AB边于点E2(如图②),记∠ADE2=α2;
(iii)作∠CDE2的平分线交BC边于点E3(如图③),记∠CDE3=α3;
按此作法从操作(2)起重复以上步骤,得到α1 , α2 , …,αn , …,现有如下结论:①当α1=10°时,α2=40°;②2α4+α3=90°; ③当α5=30°时,△CDE9≌△ADE10;④当α1=45°时,BE2= .
其中正确的个数为( )
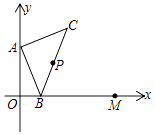
如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,取BC的中点P.当点B从点O向x轴正半轴移动到点M(2,0)时,则点P移动的路线长为.
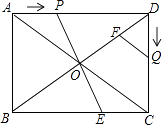
已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:
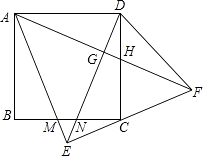
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.
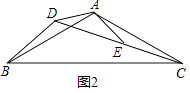
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长.
观察猜想
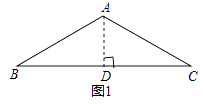
如图1,当点D在线段BC上时,
①BC与CF的位置关系为:.
②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)

数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.

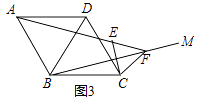
拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2 ,CD=
BC,请求出GE的长.
