 B .
B .  C .
C .  D .
D . 

|
年龄 |
人数 |
男性占比 |
|
|
4 |
50% |
|
|
|
60% |
|
|
25 |
60% |
|
|
8 |
75% |
|
|
3 |
100% |
|
第x天 |
1 |
2 |
3 |
4 |
5 |
|
销售价格p(元/只) |
2 |
3 |
4 |
5 |
6 |
|
销量q(只) |
70 |
75 |
80 |
85 |
90 |
物价部门发现这种乱象后,统一规定各药店该型号口罩的销售价格不得高于1元/只,该药店从第6天起将该型号口罩的价格调整为1元/只.据统计,该药店从第6天起销量q(只)与第 天的关系为
(
,且
为整数),已知该型号口罩的进货价格为0.5元/只.
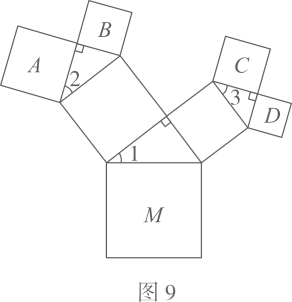
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)




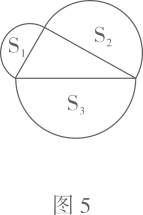

②如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为 ,
,直角三角形面积为
,请判断
,
,
的关系并证明;

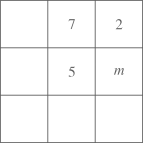
① ;
②b与c的关系为,a与d的关系为.