初中数学青岛版九年级上学期第2章 2.5解直角三角形的应用

更新时间：2020-09-03 浏览次数：158 类型：同步测试

一、单选题

1. (2020·大通模拟) 如图所示，渔船在A处看到灯塔C在北偏东60º方向上，渔船向正东方向航行了12海里到达B处，在B处看到灯塔C在正北方向上，这时渔船与灯塔C的距离是（）

A . $\text{[math]}$ 海里 B . $\text{[math]}$ 海里 C . 6海里 D . $\text{[math]}$ 海里

答案解析收藏纠错 + 选题
2. (2022·花都模拟) 如图， $\text{[math]}$ 是河堤横断面的迎水坡，堤高 $\text{[math]}$ ，水平距离 $\text{[math]}$ ，则斜坡 $\text{[math]}$ 的坡度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020·大通模拟) 如图，要测量小河两岸相对的两点 $\text{[math]}$ 之间的距离，可以在小河边 $\text{[math]}$ 的垂线 $\text{[math]}$ 上取一点C，测得 $\text{[math]}$ 米， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
4. (2020九上·茌平月考) 如图，一河坝的横断面为等腰梯形ABCD，坝顶宽10米，坝高12米，斜坡AB的坡度i＝1∶1.5，则坝底AD的长度为（）

A . 26米 B . 28米 C . 30米 D . 46米

答案解析收藏纠错 + 选题
5. (2020·铁西模拟) 如图某公园入口有三级台阶，每级台阶高18cm，深30cm，拟将台阶改为斜坡设台阶的起点为A，斜坡的起始点为C，现设计斜坡BC的坡度i=1：5，则AC的长度是（）

A . 270cm B . 210cm C . 180cm D . 96cm

答案解析收藏纠错 + 选题
6. (2020·涪城模拟) 如图，从A处观测铁塔顶部的仰角是30°，向前走30米到达B处，观测铁塔的顶部的仰角是45°，则铁塔高度是（）米

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九下·镇江月考) 一艘轮船从港口O出发，以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处，此时观测到其正西方向50海里处有一座小岛B．若以港口O为坐标原点，正东方向为x轴的正方向，正北方向为y轴的正方向，1海里为1个单位长度建立平面直角坐标系（如图），则小岛B所在位置的坐标是（）

A . （30 $\text{[math]}$ -50，30） B . （30，30 $\text{[math]}$ -50） C . （30 $\text{[math]}$ ，30） D . （30，30 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
8. (2020·皇姑模拟) 如图，小亮为了测量校园里教学楼AB的高度，将测角仪CD竖直放置在与教学楼水平距离为18 $\text{[math]}$ m的地面上，若测角仪的高度为1.5m，测得教学楼的顶部A处的仰角为30°，则教学楼的高度是（）

A . 55.5m B . 54m C . 19.5m D . 18m

答案解析收藏纠错 + 选题
9. (2023·鹿城模拟) 如图为一节楼梯的示意图，BC⊥AC，∠BAC=α，AC=6米。现要在楼梯上铺一块地毯，楼梯宽度为1米，则地毯的面积至少需要（）平方米。

A . 6tanα+6 B . $\text{[math]}$ +6 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020·温州模拟) 如图，热气球的探测器显示，从热气球A处看一栋楼顶部B处的仰角度数为α，看这栋楼底部C处的俯角度数为β，热气球A处与楼的水平距离为100m，则这栋楼的高度表示为（）

A . 100(tanα+tanβ)m B . 100(sinα+sinβ)m C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2021八上·杭州期末) 如图，在距离铁轨200米处的 $\text{[math]}$ 处，观察由南宁开往百色的“和谐号”动车，当动车车头在 $\text{[math]}$ 处时，恰好位于 $\text{[math]}$ 处的北偏东 $\text{[math]}$ 方向上，10秒钟后，动车车头到达 $\text{[math]}$ 处，恰好位于 $\text{[math]}$ 处西北方向上，则这时段动车的平均速度是（）米/秒.

A . $\text{[math]}$ B . $\text{[math]}$ C . 200 D . 300

答案解析收藏纠错 + 选题
12. (2020·衡水模拟) 已知B港口位于A观测点北偏东45°方向，且其到A观测点正北风向的距离BM的长为10 $\text{[math]}$ km，一艘货轮从B港口沿如图所示的BC方向航行4 $\text{[math]}$ km到达C处，测得C处位于A观测点北偏东75°方向，则此时货轮与A观测点之间的距离AC的长为（　　）km．

A . 8 $\text{[math]}$ B . 9 $\text{[math]}$ C . 6 $\text{[math]}$ D . 7 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2020·阜新) 如图，为了了解山坡上两棵树间的水平距离，数学活动小组的同学们测得该山坡的倾斜角 $\text{[math]}$ ，两树间的坡面距离 $\text{[math]}$ ，则这两棵树的水平距离约为m（结果精确到 $\text{[math]}$ ，参考数据： $\text{[math]}$ ）.

答案解析收藏纠错 + 选题
14. (2020·自贡) 如图，我市在建高铁的某段路基横断面为梯形 $\text{[math]}$ ， $\text{[math]}$ ∥ $\text{[math]}$ ， $\text{[math]}$ 长为6米，坡角 $\text{[math]}$ 为45°， $\text{[math]}$ 的坡角 $\text{[math]}$ 为30°，则 $\text{[math]}$ 的长为米（结果保留根号）

答案解析收藏纠错 + 选题
15. (2020九下·吉林月考) 如图，岸边的点A处距水面的高度AB为2.17米，桥墩顶部点C距水面的高度CD为12.17米．从点A处测得桥墩顶部点C的仰角为 $\text{[math]}$ ，则AC的长为米（用三角函数表示）．

答案解析收藏纠错 + 选题
16. (2020·潮阳模拟) 观光塔是某市区的标志性建筑，为测量其高度，如图，一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°，然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°。已知楼房高AB是45m，根据以上观测数据可求观光塔的高CD是m。

答案解析收藏纠错 + 选题
17. (2020·北京模拟) 如图，小军在A时测量某树的影长时，日照的光线与地面的夹角恰好是60°，当他在B时测量该树的影长时，日照的光线与地面的夹角是30°，若两次测得的影长之差 $\text{[math]}$ 为 $\text{[math]}$ ，则树的高度为 $\text{[math]}$ ．（结果精确到0.1，参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题
18. (2020·宝安模拟) 如图，从甲楼顶部A处测得乙楼顶部D处的俯角α为30°，又从A处测得乙楼底部C处的俯角β为60°，已知两楼之间的距离BC为18米，则乙楼CD的高度为米。（结果保留根号）

答案解析收藏纠错 + 选题
19. (2020·历下模拟) 如图，一游人由山脚A沿坡角为30°的山坡AB行走600m，到达一个景点B，再由B沿山坡BC行走200m到达山顶C，若在山顶C处观测到景点B的俯角为45°，则山高CD=（结果用根号表示）．

答案解析收藏纠错 + 选题
20. (2022·朝阳模拟) 某型号飞机的机翼形状如图所示，根据图中数据计算 $\text{[math]}$ 的长为 $\text{[math]}$ .（结果保留根号）

答案解析收藏纠错 + 选题

三、解答题

21. (2020·锦江模拟) 为保障师生复学复课安全，某校利用热成像体温检测系统，对入校师生进行体温检测．如图是测温通道示意图，在测温通道侧面A点测得∠DAB＝49°，∠CAB＝35°．若AB＝3m，求显示牌的高度DC．（sin35°≈0.57，tan35°≈0.70，sin49°＝0.75，tan49°≈1.15，结果精确到0.1m）．

答案解析收藏纠错 + 选题
22. (2020·呼伦贝尔) $\text{[math]}$ 两地间有一段笔直的高速铁路，长度为 $\text{[math]}$ ．某时发生的地震对地面上以点C为圆心， $\text{[math]}$ 为半径的圆形区域内的建筑物有影响．分别从 $\text{[math]}$ 两地处测得点C的方位角如图所示， $\text{[math]}$ ．高速铁路是否会受到地震的影响．请通过计算说明理由．

答案解析收藏纠错 + 选题
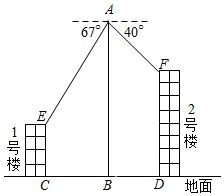
23. (2021九上·瓦房店月考) 在数学实践与综合课上，某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践，如图为实践时绘制的截面图．无人机从地面点B垂直起飞到达点A处，测得1号楼顶部E的俯角为67°，测得2号楼顶部F的俯角为40°，此时航拍无人机的高度为60米，已知1号楼的高度为20米，且EC和FD分别垂直地面于点C和D ，点B为CD的中点，求2号楼的高度．（结果精确到0.1）（参考数据sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin67°≈0.92，cos67°≈0.39，tan67°≈2.36）

答案解析收藏纠错 + 选题
24. (2020·徐州模拟) 如图，一艘船以每小时30海里的速度向北偏东75°方向航行，在点 $\text{[math]}$ 处测得码头 $\text{[math]}$ 的船的东北方向，航行40分钟后到达 $\text{[math]}$ 处，这时码头 $\text{[math]}$ 恰好在船的正北方向，在船不改变航向的情况下，求出船在航行过程中与码头 $\text{[math]}$ 的最近距离.（结果精确的0.1海里，参考数据 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
25. (2020·东丽模拟) 如图，甲楼AB高20米，乙楼CD高10米，两栋楼之间的水平距离BD＝30m ，为了测量某电视塔EF的高度，小明在甲楼楼顶A处观测电视塔塔顶E ，测得仰角为37°，小明在乙楼楼顶C处观测电视塔塔顶E ，测得仰角为45°，求该电视塔的高度EF ．
（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
26. (2022·青岛模拟) 如图，在港口A处的正东方向有两个相距 $\text{[math]}$ 的观测点B、C，一艘轮船从A处出发，北偏东 $\text{[math]}$ 方向航行至D处，在B、C处分别测得 $\text{[math]}$ ， $\text{[math]}$ 求轮船航行的距离AD (参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
27. (2022·单县模拟) 如图，我国某海域有A，B两个港口，相距80海里，港口B在港口A的东北方向，点 $\text{[math]}$ 处有一艘货船，该货船在港口A的北偏西30°方向，在港口B的北偏西75°方向，求货船与港口A之间的距离.（结果保留根号）

答案解析收藏纠错 + 选题
28. (2021·娄底模拟) 如图，小岛 $\text{[math]}$ 和 $\text{[math]}$ 都在码头 $\text{[math]}$ 的正北方向上，它们之间距离为 $\text{[math]}$ ，一艘渔船自西向东匀速航行，行驶到位于码头 $\text{[math]}$ 的正西方向 $\text{[math]}$ 处时，测得 $\text{[math]}$ ，渔船速度为 $\text{[math]}$ ，经过 $\text{[math]}$ ，渔船行驶到了 $\text{[math]}$ 处，测得 $\text{[math]}$ ，求渔船在 $\text{[math]}$ 处时距离码头 $\text{[math]}$ 有多远？（结果精确到 $\text{[math]}$ ）
（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题