湘教版备考2021年中考数学三轮复习专题11圆

更新时间：2021-05-17 浏览次数：119 类型：三轮冲刺

一、单选题

1. 如图点A，D，G，B在半圆上，四边形ABOC，DEOF，HMNO均为矩形，设BC=a， EF=b， NH=c，则下列说法正确的是（）

A . a＞b＞c B . a＝b＝c C . c＞a＞b D . b＞c＞a

答案解析收藏纠错 + 选题
2.
如图，点P为正方形ABCD的边CD上一点，BP的垂直平分线EF分别交BC、AD于E、F两点，GP⊥EP交AD于点G，连接BG交EF于点 H，下列结论：①BP=EF；②∠FHG=45°；③以BA为半径⊙B与GP相切；④若G为AD的中点，则DP=2CP．其中正确结论的序号是（　　）

A . ①②③④ B . 只有①②③ C . 只有①②④ D . 只有①③④

答案解析收藏纠错 + 选题
3. (2022九上·沭阳月考) 一个点到圆的最大距离为11cm，最小距离为5cm，则圆的半径为（）

A . 16cm或6cm， B . 3cm或8cm C . 3cm D . 8cm

答案解析收藏纠错 + 选题
4. 已知矩形ABCD的边AB＝15，BC＝20，以点B为圆心作圆，使A，C，D三点至少有一点在⊙B内，且至少有一点在⊙B外，则⊙B的半径r的取值范围是（）

A . r＞15 B . 15＜r＜20 C . 15＜r＜25 D . 20＜r＜25

答案解析收藏纠错 + 选题
5. (2017·淄川模拟) 如图，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，以此类推，依此类推，图10中有10个直角三角形的内切圆，它们的面积分别记为S₁ ， S₂ ， S₃ ， …，S₁₀ ，则S₁+S₂+S₃+…+S₁₀=（）

A . 4π B . 3π C . 2π D . π

答案解析收藏纠错 + 选题
6. (2020九上·遵化期末)
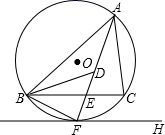
如图，在锐角△ABC中，∠A=60°，∠ACB=45°，以BC为弦作⊙O，交AC于点D，OD与BC交于点E，若AB与⊙O相切，则下列结论：
①∠BOD=90°；②DO∥AB；③CD=AD；④△BDE∽△BCD；⑤ $\text{[math]}$ = $\text{[math]}$
正确的有（　　）

A . ①② B . ①④⑤ C . ①②④⑤ D . ①②③④⑤

答案解析收藏纠错 + 选题
7.
如图，BC是⊙O的直径，AD是⊙O的切线，切点为D，AD与CB的延长线交于点A，∠C=30°，给出下面四个结论：
①AD=DC；②AB=BD；③AB= $\text{[math]}$ BC；④BD=CD，其中正确的个数为（　　）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
8.
如图，在矩形ABCD中，CD=1，∠DBC=30°．若将BD绕点B旋转后，点D落在DC延长线上的点E处，点D经过的路径，则图中阴影部分的面积是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 将边长为3cm的正三角形各边三等分，以这六个分点为顶点构成一个正六边形，则这个正六边形的面积为( )

A . $\text{[math]}$ cm2　 B . $\text{[math]}$ cm2　 C . $\text{[math]}$ cm2　 D . $\text{[math]}$ cm2

答案解析收藏纠错 + 选题
10. 如图，在⊙O中，AB是⊙O的直径，AB=10， $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，点E是点D关于AB的对称点，M是AB上的一动点，下列结论：①∠BOE=60°；②∠CED= $\text{[math]}$ ∠DOB；③DM⊥CE；④CM+DM的最小值是10，上述结论中正确的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
11. 如图，⊙O的直径AB=10，E在⊙O内，且OE=4，则过E点所有弦中，长度为整数的条数为（）

A . 4 B . 6 C . 8 D . 10

答案解析收藏纠错 + 选题
12. 如图，正方形ABCD的边AB=1， $\text{[math]}$ 和 $\text{[math]}$ 都是以1为半径的圆弧，则无阴影两部分的面积之差是（）

A . $\text{[math]}$ B . 1﹣ $\text{[math]}$ C . $\text{[math]}$ ﹣1 D . 1﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2018·黔西南模拟) 已知⊙O的半径为2，点P是⊙O内一点，且OP= $\text{[math]}$ ，过P作互相垂直的两条弦AC、BD，则四边形ABCD面积的最大值为（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
14. 如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD=120°，AB=AD=2，则⊙O的半径长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

15. (2020九上·长沙期末) 如图， $\text{[math]}$ 是锐角 $\text{[math]}$ 的外接圆， $\text{[math]}$ 是 $\text{[math]}$ 的切线，切点为F， $\text{[math]}$ ，连结 $\text{[math]}$ 交 $\text{[math]}$ 于E， $\text{[math]}$ 的平分线 $\text{[math]}$ 交 $\text{[math]}$ 于D，连结 $\text{[math]}$ ．下列结论：① $\text{[math]}$ 平分 $\text{[math]}$ ；②连接 $\text{[math]}$ ，点F为 $\text{[math]}$ 的外心；③ $\text{[math]}$ ；④若点M，N分别是 $\text{[math]}$ 和 $\text{[math]}$ 上的动点，则 $\text{[math]}$ 的最小值是 $\text{[math]}$ ．其中一定正确的是(把你认为正确结论的序号都填上)．

答案解析收藏纠错 + 选题
16. 如图，四边形ABCD是⊙O的内接四边形，点D是 $\text{[math]}$ 的中点，点E是 $\text{[math]}$ 上的一点，若∠CED=40°，则∠ADC=度．

答案解析收藏纠错 + 选题
17. 如图，AB是⊙O的直径，且经过弦CD的中点H，过CD延长线上一点E作⊙O的切线，切点为F.若∠ACF=65°，则∠E=.

答案解析收藏纠错 + 选题
18. 如图，正六边形ABCDEF的边长是6+4 $\text{[math]}$ ，点O₁ ， O₂分别是△ABF，△CDE的内心，则O₁O₂=．

答案解析收藏纠错 + 选题
19. 如图5，AB是半圆 O 的直径，E是BC的中点，OE交弦BC于点D，已知BC=8cm，DE=2cm，则AD的长为 cm.

答案解析收藏纠错 + 选题
20. 如图，圆锥的母线长OA为8，底面圆的半径为4.若一只蚂蚁在底面上点A处，在相对母线OC的中点B处有一只小虫，蚂蚁要捉小虫，需要爬行的最短路程为.

答案解析收藏纠错 + 选题

三、解答题

21. 如图，AB为⊙O直径，C为⊙O上一点，点D是 $\text{[math]}$ 的中点，DE⊥AC于E，DF⊥AB于F．
1. （1）判断DE与⊙O的位置关系，并证明你的结论；
2. （2）若OF=4，求AC的长度．
答案解析收藏纠错 + 选题
22. (2016·岳阳)
数学活动﹣旋转变换
1. （1）如图①，在△ABC中，∠ABC=130°，将△ABC绕点C逆时针旋转50°得到△A′B′C，连接BB′，求∠A′B′B的大小；
2. （2）如图②，在△ABC中，∠ABC=150°，AB=3，BC=5，将△ABC绕点C逆时针旋转60°得到△A′B′C，连接BB′，以A′为圆心，A′B′长为半径作圆．
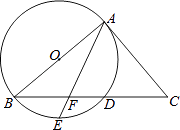
  ①猜想：直线BB′与⊙A′的位置关系，并证明你的结论；
  ②连接A′B，求线段A′B的长度；
3. （3）如图③，在△ABC中，∠ABC=α（90°＜α＜180°），AB=m，BC=n，将△ABC绕点C逆时针旋转2β角度（0°＜2β＜180°）得到△A′B′C，连接A′B和BB′，以A′为圆心，A′B′长为半径作圆，问：角α与角β满足什么条件时，直线BB′与⊙A′相切，请说明理由，并求此条件下线段A′B的长度（结果用角α或角β的三角函数及字母m、n所组成的式子表示）
答案解析收藏纠错 + 选题
23. (2018·株洲) 如图，已知AB为⊙O的直径，AB=8，点C和点D是⊙O上关于直线AB对称的两个点，连接OC、AC，且∠BOC＜90°，直线BC和直线AD相交于点E，过点C作直线CG与线段AB的延长线相交于点F，与直线AD相交于点G，且∠GAF＝∠GCE
1. （1）求证：直线CG为⊙O的切线；
2. （2）若点H为线段OB上一点，连接CH，满足CB＝CH，
  ①△CBH∽△OBC
  ②求OH＋HC的最大值
答案解析收藏纠错 + 选题
24. (2017·湘潭) 如图，动点M在以O为圆心，AB为直径的半圆弧上运动（点M不与点A、B 及 $\text{[math]}$ 的中点F 重合），连接OM．过点M 作ME⊥AB于点E，以BE为边在半圆同侧作正方形BCDE，过点M作⊙O的切线交射线DC于点N，连接BM、BN．
1. （1）
  探究：如图一，当动点M在 $\text{[math]}$ 上运动时；
  
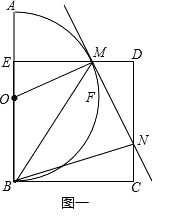
  ①判断△OEM∽△MDN是否成立？请说明理由；
  ②设 $\text{[math]}$ =k，k是否为定值？若是，求出该定值，若不是，请说明理由；
  ③设∠MBN=α，α是否为定值？若是，求出该定值，若不是，请说明理由；
2. （2）
  拓展：如图二，当动点M 在 $\text{[math]}$ 上运动时；
  
  分别判断（1）中的三个结论是否保持不变？如有变化，请直接写出正确的结论．（均不必说明理由）
答案解析收藏纠错 + 选题

四、综合题

25. (2017·冷水滩模拟) 如图，在Rt△ABC中，∠C=90°，AD是角平分线，DE⊥AD交AB于E，△ADE的外接圆⊙O与边AC相交于点F，过F作AB的垂线交AD于P，交AB于M，交⊙O于G，连接GE．
1. （1）求证：BC是⊙O的切线；
2. （2）若tan∠G= $\text{[math]}$ ，BE=4，求⊙O的半径；
3. （3）在（2）的条件下，求AP的长．
答案解析收藏纠错 + 选题
26. (2017·邗江模拟) 如图，以△ABC的边AB为直径作⊙O，与BC交于点D，点E是弧BD的中点，连接AE交BC于点F，∠ACB=2∠BAE．
1. （1）求证：AC是⊙O的切线；
2. （2）若sinB= $\text{[math]}$ ，BD=5，求BF的长．
答案解析收藏纠错 + 选题
27. (2017·苏州模拟) 如图，⊙M与菱形ABCD在平面直角坐标系中，点M的坐标为（﹣3，1），点A的坐标为（2，0），点B的坐标为（1，﹣ $\text{[math]}$ ），点D在x轴上，且点D在点A的右侧．
1. （1）求菱形ABCD的周长；
2. （2）若⊙M沿x轴向右以每秒2个单位长度的速度平移，菱形ABCD沿x轴向左以每秒3个单位长度的速度平移，设菱形移动的时间为t（秒），当⊙M与AD相切，且切点为AD的中点时，连接AC，求t的值及∠MAC的度数；
3. （3）在（2）的条件下，当点M与AC所在的直线的距离为1时，求t的值．
答案解析收藏纠错 + 选题
28. (2017·邗江模拟) 对于平面直角坐标系xOy中的点P和⊙C，给出如下定义：若存在过点P的直线l交⊙C于异于点P的A，B两点，在P，A，B三点中，位于中间的点恰为以另外两点为端点的线段的中点时，则称点P为⊙C 的相邻点，直线l为⊙C关于点P的相邻线．
1. （1）当⊙O的半径为1时，
  ①分别判断在点D（ $\text{[math]}$ ， $\text{[math]}$ ），E（0，﹣ $\text{[math]}$ ），F（4，0）中，是⊙O的相邻点有；
  ②请从①中的答案中，任选一个相邻点，在图1中做出⊙O关于它的一条相邻线，并说明你的作图过程；
  ③点P在直线y=﹣x+3上，若点P为⊙O的相邻点，求点P横坐标的取值范围；
2. （2） ⊙C的圆心在x轴上，半径为1，直线y=﹣ $\text{[math]}$ 与x轴，y轴分别交于点M，N，若线段MN上存在⊙C的相邻点P，直接写出圆心C的横坐标的取值范围．
答案解析收藏纠错 + 选题
29. (2022·莒南模拟) 如图，在Rt△ABC中，∠ACB=90°，AO是△ABC的角平分线．以O为圆心，OC为半径作⊙O．
1. （1）求证：AB是⊙O的切线．
2. （2）已知AO交⊙O于点E，延长AO交⊙O于点D，tanD= $\text{[math]}$ ，求 $\text{[math]}$ 的值．
3. （3）在（2）的条件下，设⊙O的半径为3，求AB的长．
答案解析收藏纠错 + 选题
30. (2017·泰兴模拟) 如图，△ABC内接于⊙O，BD为⊙O的直径，BD与AC相交于点H，AC的延长线与过点B的直线相交于点E，且∠A=∠EBC．
1. （1）求证：BE是⊙O的切线；
2. （2）已知CG∥EB，且CG与BD、BA分别相交于点F、G，若BG•BA=48，FG= $\text{[math]}$ ，DF=2BF，求AH的值．
答案解析收藏纠错 + 选题