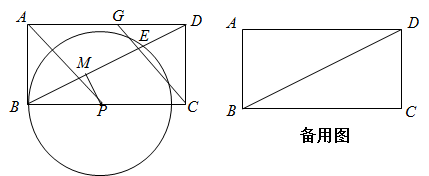
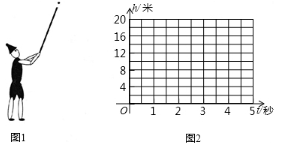
B .
B .  C .
C .  D .
D . 

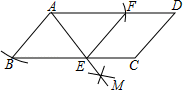

 B .
B .  C .
C .  D .
D . 
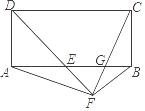



(整理数据)

“爱生活•爱运动”的活动结束之后,再次抽查这部分学生的体育锻炼时间:
| 一周体育锻炼时间(小时) | 3 | 4 | 5 | 6 | 7 |
| 人数 | 3 | 5 | 15 | a | 10 |
活动之后部分学生体育锻炼时间的统计表
(分析数据)
| 平均数 | 中位数 | 众数 | |
| 活动之前锻炼时间(小时) | 5 | 5 | 5 |
| 活动之后锻炼时间(小时) | 5.52 | b | c |
请根据调查信息分析: