

|
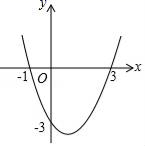
| …… | -1 | 0 | 1 | 3 | …… |
| | …… | 0 | 3 | 4 | 0 | …… |
|
x |
… |
﹣2 |
﹣1 |
0 |
1 |
2 |
… |
m |
… |
|
y |
… |
0 |
4 |
6 |
6 |
4 |
… |
﹣6 |
… |
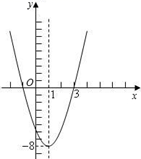
则这个二次函数的对称轴为直线x=,m=(m>0).
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
求这个二次函数的表达式,并利用配方法求出此抛物线的对称轴、顶点坐标
|
x |
… |
﹣1 |
0 |
1 |
2 |
3 |
… |
|
y |
… |
3 |
0 |
﹣1 |
0 |
m |
… |
