2021年秋季浙教版数学八年级上学期期中测试模拟卷（适合嘉兴...

更新时间：2021-10-25 浏览次数：183 类型：期中考试

一、单选题

1. (2021八上·沭阳月考) 下列图形中，是轴对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021八上·青田期中) 有两根6cm ， 8cm的木棒，以这两根木棒做一个三角形，可以选用第三根木棒的长为（）

A . 2cm B . 6cm C . 14cm D . 16cm

答案解析收藏纠错 + 选题
3. (2021八上·恩平期末) 如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是（）

A . 两点确定一条直线 B . 两点之间线段最短 C . 三角形的稳定性 D . 垂线段最短

答案解析收藏纠错 + 选题
4. 下列选项中的图形与给出的图形全等的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021七下·盐城期末) 若 $\text{[math]}$ ，则下列式子成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020八上·桐城期末) 如图， $\text{[math]}$ 是等腰三角形 $\text{[math]}$ 底边 $\text{[math]}$ 上的中线， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积是（）

A . 4 B . 6 C . 8 D . 12

答案解析收藏纠错 + 选题
7. (2021八下·龙华期末) 甲、乙两位同学分别用尺规作图法作∠AOB的平分线OC，则他们两人的作图方法（）

A . 甲、乙两人均正确 B . 甲正确，乙不正确 C . 甲不正确，乙正确 D . 甲、乙两人均不正确

答案解析收藏纠错 + 选题
8. (2019八上·仙居月考) 如图，等腰Rt△ABC中，∠BAC＝90°，AD⊥BC于D ， ∠ABC的平分线分别交AC、AD于E、F两点，M为EF的中点，延长AM交BC于点N ，连接DM ，下列结论：①AE＝AF；②DF＝DN；③AE＝CN；④△AMD和△DMN的面积相等，其中错误的结论个数是（）

A . 3个 B . 2个 C . 1个 D . 0个

答案解析收藏纠错 + 选题
9. (2021八上·沈丘期末) 如图，圆柱形容器中，高为1.2 m，底面周长为1m，在容器内壁离容器底部0.3 m的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿0.3 m与蚊子相对的点A处，则壁虎捕捉蚊子的最短距离为（）m(容器厚度忽略不计).

A . 1.8 B . 1.5 C . 1.2 D . 1.3

答案解析收藏纠错 + 选题
10. (2021八上·槐荫月考) 国庆假期中，小华与同学去玩探宝游戏，按照探宝图，他们从门口 $\text{[math]}$ 处出发先往东走 $\text{[math]}$ ，又往北走 $\text{[math]}$ ，遇到障碍后又往西走 $\text{[math]}$ ，再向北走到 $\text{[math]}$ 处往东拐，仅走了 $\text{[math]}$ ，就找到了宝藏，则门口 $\text{[math]}$ 到藏宝点 $\text{[math]}$ 的直线距离是（）

A . 20km B . 14km C . 11km D . 10km

答案解析收藏纠错 + 选题

二、填空题

11. (2019七下·博白期末) “x与5的差小于4”用不等式可表示为．

答案解析收藏纠错 + 选题
12. (2020八上·陈仓期末) 命题“若a²＞b² ，则a＞b”的逆命题是，该逆命题是（填“真”或“假”）命题.

答案解析收藏纠错 + 选题
13. (2021八下·南岸期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 的角平分线， $\text{[math]}$ ，垂足为E，若 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2021八下·城阳期末) 如图，在△ABC中，∠C =45°，AB的垂直平分线交AB于点E ，交BC于点D；AC的垂直平分线交AC于点G ，交BC于点F ，连接 AD ， AF ．若AF=2cm，BC=8cm，则DF=cm．

答案解析收藏纠错 + 选题
15. (2021八上·汉阴期末) 如图，△ABC中，点P、点Q是边BC上的两个点，若BP=PQ=QC=AP=AQ ，则∠PAC的度数为°．

答案解析收藏纠错 + 选题
16. (2020八上·淮阳期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心，适当长为半径作弧，交 $\text{[math]}$ 于 $\text{[math]}$ 两点，再分别以 $\text{[math]}$ 两点为圆心，大于 $\text{[math]}$ 的长为半径作弧，两弧相交于点 $\text{[math]}$ ，作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，则点 $\text{[math]}$ 与线段 $\text{[math]}$ 上的点的连线中，长度最短的线段的长为.

答案解析收藏纠错 + 选题

三、解答题

17. (2021八上·汉滨期中) 作图题（保留作图痕迹）已知： $\text{[math]}$ 和两点M、N，求作：一点P，使点P到 $\text{[math]}$ 两边的距离相等，且 $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2021·大连) 如图，点A ， D ， B ， E在一条直线上 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. 如图，在一条东西走向的河流的一侧有一村庄C，河边原有两个取水点A，B，其中AB=AC，由于某种原因，由C到A的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上)，并新修一条路CH，测得CB=1.5千米，CH=1.2千米，HB=0.9千米．
1. （1）试判断△CHB是不是直角三角形，并说明理由；
2. （2）求新路CH比原路CA短多少千米．
答案解析收藏纠错 + 选题
20. (2021八上·徐闻期中) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 经过点C，且 $\text{[math]}$ 于D， $\text{[math]}$ 于E，
1. （1）当直线 $\text{[math]}$ 绕点C旋转到图1的位置时，求证：
  ① $\text{[math]}$ ；
  
  ② $\text{[math]}$ ；
2. （2）当直线 $\text{[math]}$ 绕点C旋转到图2的位置时，猜想 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的关系，并请给出证明.
答案解析收藏纠错 + 选题
21. (2021八下·南城期中) 已知，如图△ABC为等边三角形，AE=CD，AD、BE相交于点P．
1. （1）求证： $\text{[math]}$ ；
2. （2）求∠BPQ的度数；
3. （3）若 $\text{[math]}$ 于Q，PQ=6，PE=2，求BE的长．
答案解析收藏纠错 + 选题

22. (2021八上·沭阳月考) 数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：

根据以下情境，解决下列问题：

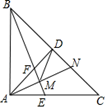
作法：①在 $\text{[math]}$ 和 $\text{[math]}$ 上分别截取 $\text{[math]}$ 、 $\text{[math]}$ ，使 $\text{[math]}$ .

②分别以D、E为圆心，以大于 $\text{[math]}$ 的长为半径作弧，两弧在 $\text{[math]}$ 内交于点C.

③作射线 $\text{[math]}$ .则 $\text{[math]}$ 就是 $\text{[math]}$ 的平分线.

（1）李老师用尺规作角平分线时，用到的三角形全等的判定方法是.
小聪只带了直角三角板，他发现利用三角板也可以作角平分线，方法如下：

步骤：①利用三角板上的刻度，在 $\text{[math]}$ 和 $\text{[math]}$ 上分别截取 $\text{[math]}$ 、 $\text{[math]}$ ，使 $\text{[math]}$ .

②分别过M、N作 $\text{[math]}$ 、 $\text{[math]}$ 的垂线，交于点P.

③作射线 $\text{[math]}$ .则 $\text{[math]}$ 为 $\text{[math]}$ 的平分线.
（2）小聪的作法正确吗？请说明理由.

答案解析收藏纠错 + 选题

23. (2019八上·长兴月考) 如图
1. （1）如图①，在四边形ABCD中，AB∥CD，点E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，DC之间的等量关系。
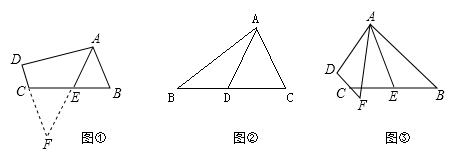
  解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC得到AB=FC，从而把AB，AD，DC转化在一个三角形中即可判断。
  
  AB，AD，DC之间的等量关系；
2. （2）同题探究；
  ①如图②，AD是△ABC的中线，AB=6，AC=4，求AD的范围：
  
  ②如图③，在四边形ABCD中，AB∥CD，AF与DC的延长线交于点F，点E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论。
答案解析收藏纠错 + 选题
24. (2021八上·泰州月考) 阅读与理解：
折纸，常常能为证明一个命题提供思路和方法.例如，在△ABC中，AB＞AC（如图），怎样证明∠C＞∠B呢？

分析：把AC沿∠A的角平分线AD翻折，因为AB＞AC，所以点C落在AB上的点C'处，即AC=AC'，据以上操作，易证明△ACD≌△AC'D，所以∠AC'D=∠C，又因为∠AC'D＞∠B，所以∠C＞∠B.

感悟与应用：
1. （1）如图（a），在△ABC中，∠ACB=90°，∠B=30°，CD平分∠ACB，试判断AC和AD、BC之间的数量关系，并说明理由；
2. （2）如图（b），在四边形ABCD中，AC平分∠BAD，AC=16，AD=8，DC=BC=12，
  ①求证：∠B+∠D=180°；
  
  ②求AB的长.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2021年秋季浙教版数学八年级上学期期中测试模拟卷（适合嘉兴...

副标题：

*注意事项：

2021年秋季浙教版数学八年级上学期期中测试模拟卷（适合嘉兴...

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析