2021年秋季浙教版数学九年级上学期期中测试模拟卷（适合杭州...

更新时间：2021-10-25 浏览次数：243 类型：期中考试

一、单选题

1. (2021九上·上海月考) 已知点C在线段AB的延长线上，5CB=2AC，则AB：AC=（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020九上·镇海区期中) 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为圆上的三点， $\text{[math]}$ ， $\text{[math]}$ 点可能是圆心的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. 有一个质地均匀且可以转动的转盘，盘面被分成6个全等的扇形区域，在转盘的适当地方涂上灰色，未涂色部分为白色，用力转动转盘，为了使转盘停止时，指针指向灰色的可能性的大小是 $\text{[math]}$ ，那么下列涂色方案正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021·萧山模拟) 平面直角坐标系中有两条抛物线 $\text{[math]}$ 与 $\text{[math]}$ ，其中 $\text{[math]}$ .下列三个结论中：
①如果抛物线 $\text{[math]}$ 与x轴的一个交点为 $\text{[math]}$ ，那么 $\text{[math]}$ 是抛物线 $\text{[math]}$ 与x轴的一个交点；

②如果当 $\text{[math]}$ 时 $\text{[math]}$ 随x的增大而增大，那么当 $\text{[math]}$ 时 $\text{[math]}$ 也随x的增大而增大；

③如果 $\text{[math]}$ ，那么x的取值范围为 $\text{[math]}$ .

其中正确结论是（　　）

A . ①② B . ①③ C . ②③ D . ①②③

答案解析收藏纠错 + 选题
5. (2021·东城模拟) 在平面直角坐标系 $\text{[math]}$ 中，⊙O的半径为2，点A（1， $\text{[math]}$ ）与⊙O的位置关系是（）

A . 在⊙O上 B . 在⊙O内 C . 在⊙O外 D . 不能确定

答案解析收藏纠错 + 选题
6. (2021九上·渝中开学考) 如图，把 $\text{[math]}$ 绕着点 $\text{[math]}$ 顺时针方向旋转 $\text{[math]}$ ，得到△ $\text{[math]}$ ，点 $\text{[math]}$ 刚好落在边 $\text{[math]}$ 上.则 $\text{[math]}$ =（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·牡丹江) 一条弧所对的圆心角为135°，弧长等于半径为3cm的圆的周长的5倍，则这条弧的半径为（）

A . 45cm B . 40cm C . 35cm D . 30cm

答案解析收藏纠错 + 选题
8. (2022·大庆模拟) 如图，已知抛物线 $\text{[math]}$ 的对称轴在 $\text{[math]}$ 轴右侧，抛物线与 $\text{[math]}$ 轴交于点 $\text{[math]}$ 和点 $\text{[math]}$ ，与 $\text{[math]}$ 轴的负半轴交于点 $\text{[math]}$ ，且 $\text{[math]}$ ，则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④当 $\text{[math]}$ 时，在 $\text{[math]}$ 轴下方的抛物线上一定存在关于对称轴对称的两点 $\text{[math]}$ ， $\text{[math]}$ （点 $\text{[math]}$ 在点 $\text{[math]}$ 左边），使得 $\text{[math]}$ .其中正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
9. (2020九上·杭州期中) 如图，⊙O的直径AB=8，P是圆上任一点（A，B除外），∠APB的平分线交⊙O于C，弦EF过AC，BC的中点M、N，则EF的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 6 D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020九上·高安期中) 已知二次函数y＝ax²﹣2ax﹣3a（a≠0），关于此函数的图象及性质，下列结论中不一定成立的是（）

A . 该图象的顶点坐标为（1，﹣4a） B . 该图象在x轴上截得的线段的长为4 C . 若该图象经过点（﹣2，5），则一定经过点（4，5） D . 当x＞1时，y随x的增大而增大

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·浦北月考) 二次函数 $\text{[math]}$ 的最小值是．

答案解析收藏纠错 + 选题
12. (2020九上·密山期末) 如图，△ABC中，D在BC上，F是AD的中点，连CF并延长交AB于E，已知 $\text{[math]}$ ，则 $\text{[math]}$ 等于．

答案解析收藏纠错 + 选题
13. (2023·徐汇模拟) 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”.如图， $\text{[math]}$ 为 $\text{[math]}$ 的黄金分割点 $\text{[math]}$ ，如果 $\text{[math]}$ 的长度为 $\text{[math]}$ ，那么 $\text{[math]}$ 的长度是.

答案解析收藏纠错 + 选题
14. (2021·大庆模拟) 如图，边长为2的等边三角形 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 内（包括 $\text{[math]}$ 的边）一动点，且满足 $\text{[math]}$ ，则点 $\text{[math]}$ 运动的路径的长度为.

答案解析收藏纠错 + 选题
15. (2021·阳西模拟) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．将矩形 $\text{[math]}$ 绕点 $\text{[math]}$ 按顺时针方向旋转得到矩形 $\text{[math]}$ ，点 $\text{[math]}$ 落在矩形 $\text{[math]}$ 的边 $\text{[math]}$ 上的点 $\text{[math]}$ 处，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
16. (2021九上·长沙开学考) 二次函数y＝ax²+bx+c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x＝2，下列结论：

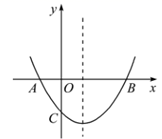
①4a+b＝0；②9a+c＞3b；③，3a+c＞0；④当x＞﹣1时，y的值随x值的增大而增大.⑤ $\text{[math]}$ （m为任意实数）其中正确的结论有.（填序号）

答案解析收藏纠错 + 选题

三、解答题

17. 已知：线段a、b、c，且 $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的值．
2. （2）如线段a、b、c满足a+b+c=27．求a、b、c的值．
答案解析收藏纠错 + 选题
18. (2021九上·通榆月考) 对于抛物线y=x²-4x+3
1. （1）将抛物线的解析式化为顶点式
2. （2） E坐标系中利用五点法画出此抛物线
  
  x
  
  ……
  
  ……
  
  y
  
  ……
  
  ……
3. （3）指出当x取什么值时，函数的值y随x的增大而增大？
答案解析收藏纠错 + 选题
19. (2021·无锡) 将4张分别写有数字1、2、3、4的卡片（卡片的形状、大小、质地都相同）放在盒子中，搅匀后从中任意取出1张卡片，记录后放回、搅匀，再从中任意取出1张卡片.求下列事件发生的概率.（请用“画树状图”或“列表”等方法写出分析过程）
1. （1）取出的2张卡片数字相同；
2. （2）取出的2张卡片中，至少有1张卡片的数字为“3”.
答案解析收藏纠错 + 选题
20. (2021·苏州) 如图，二次函数 $\text{[math]}$ （ $\text{[math]}$ 是实数，且 $\text{[math]}$ ）的图象与 $\text{[math]}$ 轴交于 $\text{[math]}$ 、 $\text{[math]}$ 两点（点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧），其对称轴与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，已知点 $\text{[math]}$ 位于第一象限，且在对称轴上， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 轴的正半轴上， $\text{[math]}$ .连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，连接 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点的坐标（用数字或含 $\text{[math]}$ 的式子表示）；
2. （2）已知点 $\text{[math]}$ 在抛物线的对称轴上，当 $\text{[math]}$ 的周长的最小值等于 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
21. (2021·百色) 如图，PM、PN是⊙O的切线，切点分别是A、B，过点O的直线CE∥PN，交⊙O于点C、D，交PM于点E，AD的延长线交PN于点F，若BC∥PM.
1. （1）求证：∠P＝45°；
2. （2）若CD＝6，求PF的长.
答案解析收藏纠错 + 选题
22. (2020九上·桐城期末) 已知抛物线 $\text{[math]}$ 可由抛物线 $\text{[math]}$ 平移得到，且经过点 $\text{[math]}$ ．
1. （1）确定 $\text{[math]}$ 的值；
2. （2）试确定该抛物线的顶点坐标．
答案解析收藏纠错 + 选题
23. (2020九上·北仑期中) 如图， $\text{[math]}$ 点为 $\text{[math]}$ 轴正半轴上一点， $\text{[math]}$ 交 $\text{[math]}$ 轴于 $\text{[math]}$ 、 $\text{[math]}$ 两点，交 $\text{[math]}$ 轴于 $\text{[math]}$ 、 $\text{[math]}$ 两点， $\text{[math]}$ 点为劣弧 $\text{[math]}$ 上一个动点，连接 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）如图1，求点 $\text{[math]}$ 的坐标和 $\text{[math]}$ 的度数；
2. （2）如图2，若 $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ 点，当 $\text{[math]}$ 点在运动时，线段 $\text{[math]}$ 的长度是否发生变化；若不变求出其值，若发生变化，求出变化的范围；
3. （3）如图3，连接 $\text{[math]}$ ，当 $\text{[math]}$ 点在运动时（不与 $\text{[math]}$ 、 $\text{[math]}$ 两点重合），求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题