



若四边形 是正方形,点P是射线
上一动点,以
为直角边在
边的右侧作等腰
,其中
.
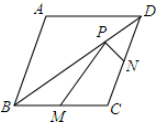
①如图2,当点 在对角线
上时,小组发现点
恰好在射线
上,求
与
之间的数量关系(过程只用说明点
在线段
上的情况即可);
②如图3,当P是对角线 的延长线上一动点时,小组发现点
恰好在射线
上,连接
,若
,求
的面积.
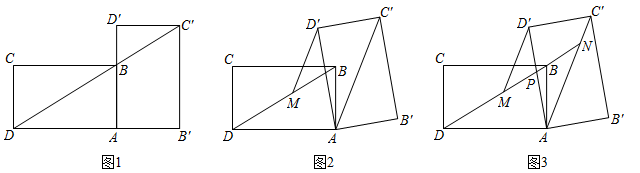
[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M . 线段D′M与DM相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P , N(如图3),发现线段DN , MN , PN存在一定的数量关系,请写出这个关系式,并加以证明.
试题篮
0