
|
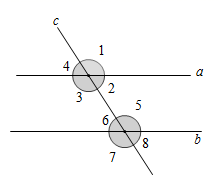
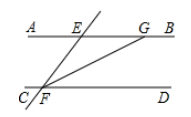
如图,已知直线 请完成下面的说理过程. 解:已知 根据(内错角相等,两直线平行),得 再根据( ※ ),得 |
|
①同位角相等;
②一条直线有无数条平行线;
③在同一平面内,两条不相交的线段是平行线;
④如果 ,
,则
;
⑤过一点有且只有一条直线与已知直线平行.





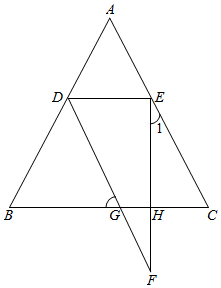

求证:∠A=∠D;

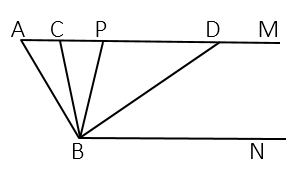
②∵AM //BN,∴∠ACB=∠;

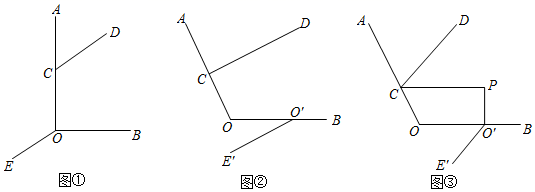
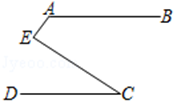
如图①,已知:AB∥CD,E为AB、CD之间一点,连接BE,ED,得到∠BED.
求证:∠BED=∠B+∠D.
小亮帮助小明给出了该问的证明.
证明:
过点E作EF∥AB
则有∠BEF=∠B
∵AB∥CD
∴EF∥CD
∴∠FED=∠D
∴∠BED=∠BEF+∠FED=∠B+∠D
请你参考小亮的思考问题的方法,解决问题: