 B .
B .  C .
C . 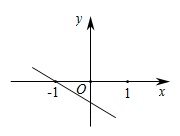 D .
D . 
| | … | -1 | 0 | 2 | 4 | 5 | 6 | … |
| | … | -2 | 1 | 7 | 11 | 16 | 19 | … |


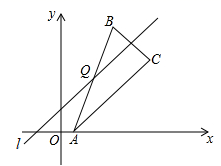




①若点P在x轴正半轴上,则点P的坐标是 ;
②若点P在第一象限,且∠PAO=30°,求点P的坐标;