苏科版初中数学七年级下册 12.2 证明同步训练（基础版）

更新时间：2022-03-23 浏览次数：101 类型：同步测试

一、单选题

1. 用反证法证明命题：“如图，如果AB//CD，AB//EF，那么CD//EF.”证明的第一个步骤是（）

A . 假定CD//EF B . 假定CD不平行于EF C . 已知AB//EF D . 假定AB不平行于EF

答案解析收藏纠错 + 选题

2. (2021八上·于洪期末) 定理：三角形的一个外角等于与它不相邻的两个内角的和．已知：如图，∠ACD是△ABC的外角．求证：∠ACD＝∠A+∠B．

证法1：如图，

∵∠A＝70°，∠B＝63°，

且∠ACD＝133°（量角器测量所得）

又∵133°＝70°+63°（计算所得）

∴∠ACD＝∠A+∠B（等量代换）．

证法2：如图，

∵∠A+∠B+∠ACB＝180°（三角形内角和定理），

又∵∠ACD+∠ACB＝180°（平角定义），

∴∠ACD+∠ACB＝∠A+∠B+∠ACB（等量代换）．

∴∠ACD＝∠A+∠B（等式性质）．

下列说法正确的是（）

A . 证法1用特殊到一般法证明了该定理 B . 证法1只要测量够100个三角形进行验证，就能证明该定理 C . 证法2还需证明其他形状的三角形，该定理的证明才完整 D . 证法2用严谨的推理证明了该定理

答案解析收藏纠错 + 选题

3. (2021八上·沂水期中) 在探究证明“三角形的内角和是180°”时，综合实践小组的同学作了如下四种辅助线，其中不能证明“三角形内角和是180°”的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021七上·平阳期中) 如图，给出下列条件：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ，且 $\text{[math]}$ ；④ $\text{[math]}$ 且 $\text{[math]}$ ；其中能推出 $\text{[math]}$ 的条件为（）

A . ①② B . ②④ C . ②③ D . ②③④

答案解析收藏纠错 + 选题

5. (2021·荆州) 阅读下列材料，其①～④步中数学依据错误的是（）

如图：已知直线 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ .

证明：①∵ $\text{[math]}$ （已知）

∴ $\text{[math]}$ （垂直的定义）

②又∵ $\text{[math]}$ （已知）

③∴ $\text{[math]}$ （同位角相等，两直线平行）

∴ $\text{[math]}$ （等量代换）

④∴ $\text{[math]}$ （垂直的定义）.

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题

6. (2020七下·济南期中) 如图，点E在BA的延长线上，能证明BE∥CD是（）

A . ∠EAD=∠B B . ∠BAD=∠BCD C . ∠EAD=∠ADC D . ∠BCD+∠D=180°

答案解析收藏纠错 + 选题
7. (2020七上·道外期末) 如图，下列条件中能证明AD $\text{[math]}$ BC的是（）

A . ∠A＝∠C B . ∠ABE＝∠C C . ∠A+∠D＝180° D . ∠C+∠D＝180°

答案解析收藏纠错 + 选题
8. (2020七下·吉林期中) 已知a，b，c是三条直线，下列结论正确的是（）

A . 若a∥b，b∥c，则a∥c B . 若a⊥b，b⊥c，则a⊥c C . 若a∥b，b⊥c，则a∥c D . 若a⊥b，b∥c，则a∥c

答案解析收藏纠错 + 选题
9. (2020八上·达县期末) 如图，下列推理及所证明的理由都正确的是（）

A . 若 $\text{[math]}$ ，则 $\text{[math]}$ ，理由是内错角相等，两直线平行 B . 若 $\text{[math]}$ ，则 $\text{[math]}$ ，理由是两直线平行，内错角相等 C . 若 $\text{[math]}$ ，则 $\text{[math]}$ ，理由是内错角相等，两直线平行 D . 若 $\text{[math]}$ ，则 $\text{[math]}$ ，理由是两直线平行，内错角相等

答案解析收藏纠错 + 选题
10. 下列选项中，可以用来证明命题“若a2-4a=0，则a=0”是假命题的反例是（）.

A . a = -2 B . a = -1 C . a = 4 D . a = 2

答案解析收藏纠错 + 选题

二、填空题

11. (2021八上·诸暨月考) 命题“若x（1﹣x）＝0，则x＝0”是命题（填“真”、假），证明时可举出的反例是．

答案解析收藏纠错 + 选题
12. (2021七下·海淀期中) 完成下面的证明：已知：如图， $\text{[math]}$ ．求证： $\text{[math]}$ ∥ $\text{[math]}$ ．

证明：过点 $\text{[math]}$ 作 $\text{[math]}$ ∥ $\text{[math]}$ ．

$\text{[math]}$      ▲   （       ）．

$\text{[math]}$ ，

$\text{[math]}$ ．

$\text{[math]}$     ▲   ∥    ▲   （          ）．

$\text{[math]}$ ∥ $\text{[math]}$ （       ）．

答案解析收藏纠错 + 选题
13. (2020七上·宜兴期中) 取一个自然数，若它是奇数，则乘以3加上1，若它是偶数，则除以2，按此规则经过若干步的计算最终可得到1．这个结论在数学上还没有得到证明．但举例验证都是正确的．例如：取自然数5．最少经过下面5步运算可得1，即： $\text{[math]}$ ，如果自然数 $\text{[math]}$ 最少经过7步运算可得到1，则所有符合条件的 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
14. (2020八上·呼和浩特期末) 如图，等边三角形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ 平分 $\text{[math]}$ ，且交 $\text{[math]}$ 于 $\text{[math]}$ .如果用“三角形三条角平分线必交于一点”来证明 $\text{[math]}$ 也一定平分 $\text{[math]}$ ，那么必须先要证明．

答案解析收藏纠错 + 选题
15. (2020七下·门头沟期末) 完成下面的证明：
1. （1）已知：如图，AB∥CD
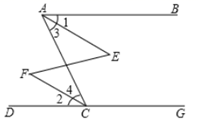
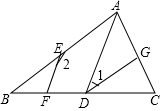
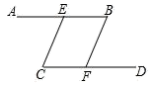
  求证：∠1+∠3 = 180°
  
  证明：∵ AB∥CD（已知），
  
  ∴ ∠1+∠2 = 180°（）
  
  又∵ ∠2 = ∠3（）
  
  ∴ ∠1+∠3=180°（）
2. （2）已知：如图，AM∥EF ， ∠1 = ∠B ．
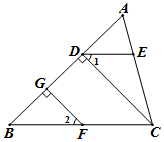
  求证：∠2 = ∠C ．
  
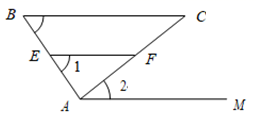
  证明：∵ ∠1 = ∠B（已知），
  
  ∴ EF∥BC（）
  
  ∵ AM∥EF（已知），
  
  ∴ AM∥BC（）
  
  ∴ ∠2 = ∠C（）
答案解析收藏纠错 + 选题
16. (2019·朝阳模拟) 在数学活动课上，老师说有人根据如下的证明过程，得到“1＝2”的结论．
设a、b为正数，且a＝b．

∵a＝b，

∴ab＝b² ．      ①

∴ab﹣a²＝b²﹣a² ．     ②

∴a（b﹣a）＝（b+a）（b﹣a）．    ③

∴a＝b+a．         ④

∴a＝2a．      ⑤

∴1＝2．                                         ⑥

大家经过认真讨论，发现上述证明过程中从某一步开始出现不正确，这一步是（填入编号），造成不正确原因是．

答案解析收藏纠错 + 选题

三、解答题

17. (2021七下·珠海期中) 如图所示，∠B＝∠C，AB∥CD，证明：CE∥BF.

答案解析收藏纠错 + 选题
18. (2022七下·深圳月考) 已知：如图， $\text{[math]}$ ， $\text{[math]}$ .
求证： $\text{[math]}$ ∥ $\text{[math]}$ .

答案解析收藏纠错 + 选题
19. (2021七下·黄陂期末) 如图， $\text{[math]}$ ，点 $\text{[math]}$ 为直线 $\text{[math]}$ ， $\text{[math]}$ 的交点， $\text{[math]}$ .
求证： $\text{[math]}$ .

答案解析收藏纠错 + 选题
20. (2021七下·鄞州期末) 如图，已知 $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点E， $\text{[math]}$ .
1. （1）证明： $\text{[math]}$
2. （2）若 $\text{[math]}$ 于点D， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
答案解析收藏纠错 + 选题
21. (2021七下·仪征期末) 已知：如图，CD⊥AB，FG⊥AB，垂足分别为D、G，点E在AC上，且∠1＝∠2.
1. （1）求证：DE $\text{[math]}$ BC；
2. （2）如果∠B＝46°，且∠A比∠ACB小10°，求∠DEC的度数.
答案解析收藏纠错 + 选题
22. (2021七下·北仑期中) 如图，已知直线AB∥CD ，直线MN分别交AB、CD于M、N两点，若ME、NF分别是∠AMN、∠DNM的角平分线，试说明：ME∥NF
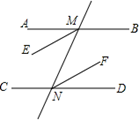
解：∵AB∥CD ，（ ▲ ）

∴∠AMN＝∠DNM（ ▲）

∵ME、NF分别是∠AMN、∠DNM的角平分线，（已知）

∴∠EMN＝ ▲∠AMN ，

∠FNM＝ ▲∠DNM （角平分线的定义）

∴∠EMN＝∠FNM（等量代换）

∴ME∥NF（ ▲）

由此我们可以得出一个结论：两条平行线被第三条直线所截，一对 ▲角的平分线互相 ▲ ．

答案解析收藏纠错 + 选题
23. (2020七下·麻城期末) 证明填空：如图，已知直线 $\text{[math]}$ ， $\text{[math]}$ ，
求证： $\text{[math]}$ .

证明： $\text{[math]}$ 已知 $\text{[math]}$

$\text{[math]}$ _▲_ $\text{[math]}$

又 $\text{[math]}$ _▲_ $\text{[math]}$

$\text{[math]}$ _▲_ $\text{[math]}$

$\text{[math]}$ _▲ $\text{[math]}$

$\text{[math]}$ _▲ $\text{[math]}$

答案解析收藏纠错 + 选题
24. (2024七下·廊坊期中) 如图，AB∥DG，∠1+∠2＝180°，
1. （1）求证：AD∥EF；
2. （2）若DG是∠ADC的平分线，∠2＝150°，求∠B的度数．
答案解析收藏纠错 + 选题