题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

2022年浙教版数学八下复习阶梯训练：反比例函数（优生集训...

更新时间：2022-04-22 浏览次数：184 类型：复习试卷

一、综合题

1. 如图所示，点A，B分别在 $\text{[math]}$ 轴、 $\text{[math]}$ 轴上，点 $\text{[math]}$ 在第一象限内， $\text{[math]}$ 轴于点 $\text{[math]}$ $\text{[math]}$ ，反比例函数 $\text{[math]}$ 的图象过CD的中点 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）求 $\text{[math]}$ 的值；
3. （3） $\text{[math]}$ 和 $\text{[math]}$ 关于某点成中心对称，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，试判断点 $\text{[math]}$ 是否在反比例函数的图象上，并说明理由.
答案解析收藏纠错 + 选题
2. 如图所示，点 $\text{[math]}$ 是反比例函数 $\text{[math]}$ 图象上的任意一点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，交另一个反比例函数 $\text{[math]}$ 的图象于点 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ，则 $\text{[math]}$ ；
2. （2）当 $\text{[math]}$ 时，若点 $\text{[math]}$ 的横坐标是1，求 $\text{[math]}$ 的度数；
3. （3）若无论点 $\text{[math]}$ 在何处，反比例函数 $\text{[math]}$ 图象上总存在一点 $\text{[math]}$ ，使得四边形AOBD为平行四边形，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
3. (2021八下·临汾期中) 如图，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ （k为常数， $\text{[math]}$ ）的图象在第一象限内交于点 $\text{[math]}$ ，且与x轴、y轴分别交于 $\text{[math]}$ 两点．
1. （1）求一次函数和反比例函数的表达式；
2. （2）点P在x轴上，且 $\text{[math]}$ 的面积等于2，求点P的坐标．
答案解析收藏纠错 + 选题
4. (2020八下·新昌期末) 如图，在平面直角坐标系中，有大正方形AOBC与小正方形CDEF，其中点A落在y轴上，点B落在x轴上，若反比例函数 $\text{[math]}$ 的图象经过点E，则称满足条件的k值为两正方形的和谐值.已知反比例函数图象与AF交于点G，请解答下列各题.
1. （1）概念理解若图中大正方形的边长为2，小正方形的边长为1，求这两个正方形的和谐值.
2. （2）性质探究记图中两正方形面积分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求证：两个正方形的和谐值 $\text{[math]}$ .
3. （3）性质应用若图中大正方形的边长为6，点G恰好是AC的三等分点，求小正方形的边长.
答案解析收藏纠错 + 选题
5. (2020八下·吴兴期末) 已知反比例函数 $\text{[math]}$ 和 $\text{[math]}$ ，过点P（0，1）作x轴的平行线l与函数 $\text{[math]}$ 的图象相交于点B，C.
1. （1）如图1，若 $\text{[math]}$ 时，求点B，C的坐标；
2. （2）如图2，一次函数 $\text{[math]}$ 交l于点D．
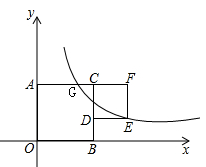
  ①若k＝5，B、C、D三点恰好满足其中一点为另外两点连线的中点，求m的值；
  
  ②过点B作y轴的平行线与函数y₃的图象相交于点E．当m值取不大于 $\text{[math]}$ 的任意实数时，点B、C间的距离与点B、E间的距离之和d始终是一个定值．求此时k的值及定值d．
答案解析收藏纠错 + 选题

6. (2020八下·房山期中) 有这样一个问题：探究函数 $\text{[math]}$ 的图象与性质．小华根据学习函数的经验，对函数 $\text{[math]}$ 的图象与性质进行了探究．下面是小华的探究过程，请补充完整：

（1）函数 $\text{[math]}$ 的自变量x的取值范围是；

（2）下表是y与x的几组对应值．m的值为；

x	-2	$\text{[math]}$	-1	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	1	2	3	4	…
y	0	$\text{[math]}$	m	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	1	$\text{[math]}$	$\text{[math]}$	…

（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的一条性质：．
（5）结合函数图象估计 $\text{[math]}$ 的解的个数为个．

答案解析收藏纠错 + 选题

7. (2020八下·泉州期中) 已知点A，B在反比例函数 $\text{[math]}$ (x>0)的图象上，它们的横坐标分别为m，n，且m≠n，过点A，点B都向x轴，y轴作垂线段，其中两条垂线段的交点为C．
1. （1）如图，当m=2，n=6时，直接写出点C的坐标：
2. （2）若A(m，n)，B(n，m)．连接OA、OB、AB，求△AOB的面积：(用含m的代数式表示)
3. （3）设AD⊥y轴于点D，BE⊥x轴于点E．若 $\text{[math]}$ ，且 $\text{[math]}$ ，则当点C在直线DE上时，求p的取值范围．
答案解析收藏纠错 + 选题
8. (2020九上·邢台期中) 在平面直角坐标系xOy中，函数 $\text{[math]}$ (x>0)的图象与直线l₁： $\text{[math]}$ 交于点A，与直线l₂：x=k交于点B.直线l₁与l₂交于点C.
1. （1）当点A的横坐标为1时，则此时k的值为；
2. （2）横、纵坐标都是整数的点叫做整点. 记函数 $\text{[math]}$ (x>0) 的图像在点A、B之间的部分与线段AC，BC围成的区域(不含边界)为W.
  ①当k=3时，结合函数图象，则区域W内的整点个数是；
  
  ②若区域W内恰有1个整点，结合函数图象，直接写出k的取值范围：.
答案解析收藏纠错 + 选题
9. (2020八下·泰兴期中) 如图，已知线段AB，A（2，1），B（4，3），现将线段AB沿y轴方向向下平移得到线段MN，直线y＝mx＋b过M、N两点，且M、N两点恰好也落在双曲线y= $\text{[math]}$ 的一条分支上，
1. （1）求反比例函数和一次函数的解析式.
2. （2）直接写出不等式mx+b－ $\text{[math]}$ ≥0的解集
3. （3）若点C（x₁ ， a），D（x₂ ， a－1）在双曲线y= $\text{[math]}$ 上，试比较x₁和x₂的大小.
答案解析收藏纠错 + 选题
10. (2020八下·泰兴期中) 在平面直角坐标系中，点A，B，C是x轴的正半轴上从左向右依次排列的三点，过点A，B，C分别作与 $\text{[math]}$ 轴平行的直线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）如图1，若直线 $\text{[math]}$ 与直线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别交于点D，E，F三点，设D（ $\text{[math]}$ ， $\text{[math]}$ ），E（ $\text{[math]}$ ， $\text{[math]}$ ），F（ $\text{[math]}$ ， $\text{[math]}$ ）.
  ①若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ （填“=”，“>”或“<”）；
  
  ②若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ （ $\text{[math]}$ ），求证：AB=BC；
2. （2）如图2，点A，B，C的横坐标分别为 $\text{[math]}$ ，n， $\text{[math]}$ （ $\text{[math]}$ ），直线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与反比例函数 $\text{[math]}$ （ $\text{[math]}$ ）的图像分别交于点D，E，F，根据以上探究的经验，探索
  $\text{[math]}$ 与 $\text{[math]}$ 之间的大小关系，并说明理由.
答案解析收藏纠错 + 选题
11. (2020八下·射阳期中) 已知一次函数 $\text{[math]}$ 和反比例函数 $\text{[math]}$ .
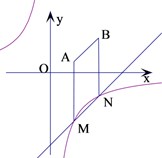
1. （1）如图1，若 $\text{[math]}$ ，且函数 $\text{[math]}$ 、 $\text{[math]}$ 的图象都经过点 $\text{[math]}$ .求m，k的值；
2. （2）如图2，过点 $\text{[math]}$ 作y轴的平行线l与函数 $\text{[math]}$ 的图象相交于点B，与反比例函数 $\text{[math]}$ 的图象相交于点C.
  $\text{[math]}$ 若 $\text{[math]}$ ，直线l与函数 $\text{[math]}$ 的图象相交点 $\text{[math]}$ 当点B、C、D中的一点到另外两点的距离相等时，求 $\text{[math]}$ 的值；
  
  $\text{[math]}$ 过点B作x轴的平行线与函数 $\text{[math]}$ 的图象相交与点 $\text{[math]}$ 当 $\text{[math]}$ 的值取不大于1的任意实数时，点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d.
答案解析收藏纠错 + 选题
12. (2020八下·扬州期中) 在平面直角坐标系xOy中，点A、B为反比例函数 $\text{[math]}$ 的图像上两点，A点的横坐标与B点的纵坐标均为1，将 $\text{[math]}$ 的图像绕原点O顺时针旋转90°，A点的对应点为A’，B点的对应点为B’.
1. （1）点A’的坐标是，点B’的坐标是；
2. （2）在x轴上取一点P，使得PA+PB的值最小，直接写出点P的坐标. 此时在反比例函数 $\text{[math]}$ 的图像上是否存在一点Q，使△A’B’Q的面积与△PAB的面积相等，若存在，求出点Q的横坐标；若不存在，请说明理由；
3. （3）连接AB’，动点M从A点出发沿线段AB’以每秒1个单位长度的速度向终点B’运动；动点N同时从B’点出发沿线段B’A’以每秒1个单位长度的速度向终点A’运动.当其中一个点停止运动时，另一个点也随之停止运动.设运动的时间为t秒，试探究：是否存在使△MNB’为等腰直角三角形的t值.若存在，求出t的值；若不存在，说明理由.
答案解析收藏纠错 + 选题
13. (2020八下·宛城期中) 已知一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于点A，与x轴交于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求反比例函数的解析式：
2. （2）若点P为x轴上一动点，当 $\text{[math]}$ 是等腰三角形时，直接写出点P的坐标.
答案解析收藏纠错 + 选题
14. (2020八下·相城期中) 如图，一次函数y=ax+b与反比例函数y= $\text{[math]}$ （x＞0)的图像在第一象限交于A、B两点，点B坐标为(4，2)，连接OA、OB，过点B作BD⊥y轴，垂足为D，交OA于点C，且OC=CA.
1. （1）求反比例函数和一次函数的表达式；
2. （2）根据图像直接说出不等式ax+b- $\text{[math]}$ ＜0的解集为；
3. （3）求△ABC的面积.
答案解析收藏纠错 + 选题
15. (2020九上·邢台期中) 阅读理解：已知：对于实数a≥0，b≥0，满足a+b≥2 $\text{[math]}$ ，当且仅当a = b时，等号成立，此时取得代数式a+b的最小值.
根据以上结论，解决以下问题：
1. （1）拓展：若a>0，当且仅当a=时，a+ $\text{[math]}$ 有最小值，最小值为；
2. （2）应用：
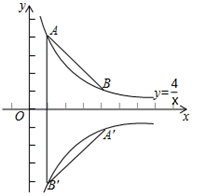
  ①如图1，已知点P为双曲线y= $\text{[math]}$ (x>0)上的任意一点，过点P作PA⊥x轴，PB丄y轴，四边形OAPB的周长取得最小值时，求出点P的坐标以及周长最小值：
  
  ②如图2，已知点Q是双曲线y= $\text{[math]}$ (x>0)上一点，且PQ∥x轴，连接OP、OQ，当线段OP取得最小值时，在平面内取一点C，使得以0、P、Q、C为顶点的四边形是平行四边形，求出点C的坐标.
答案解析收藏纠错 + 选题
16. (2020八下·江阴期中) 如图，已知一次函数y=mx+n的图像与x轴交于点B，与反比例函数 $\text{[math]}$ (k﹥0)的图像交于点C，过点C作CH⊥x轴，点D是反比例函数图象上的一点，直线CD与x轴交于点A，若∠HCB=∠HCA，且BC=10，BA=16.
1. （1）若OA=11，求k的值；
2. （2）沿着x轴向右平移直线BC，若直线经过H点时恰好又经过点D，求一次函数函数y=mx+n的表达式.
答案解析收藏纠错 + 选题
17. (2020八上·衡阳期末) 如图，若A（﹣4，n），B（2，﹣4）是一次函数y＝kx+b的图象和反比例函数y＝ $\text{[math]}$ 的图象的两个交点．
1. （1）求反比例函数和一次函数的解析式；
2. （2）求直线AB与x轴的交点C的坐标及△AOB的面积；
3. （3）观察图象，直接写出反比例函数值大于一次函数值x取值范围．
答案解析收藏纠错 + 选题
18. 如图，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点B，与双曲线 $\text{[math]}$ 交于点A，C，其中点A在第一象限，点C在第三象限.
1. （1）求B点的坐标.
2. （2）若 $\text{[math]}$ ，求A点的坐标.
3. （3）在 (2)的条件下，在坐标轴上是否存在点P，使△AOP是等腰三角形?若存在，有几个符合条件的点P?
答案解析收藏纠错 + 选题
19. 如图，A ，B两点在函数 $\text{[math]}$ 的图象上.
1. （1）求 $\text{[math]}$ 的值及直线AB对应的函数关系式.
2. （2）如果一个点的横、纵坐标均为整数，那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的个数.
答案解析收藏纠错 + 选题
20. 如图，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于 $\text{[math]}$ 两点.
1. （1）求一次函数的关系式.
2. （2）根据图象直接写出 $\text{[math]}$ 的 $\text{[math]}$ 的取值范围.
3. （3）求 $\text{[math]}$ AOB的面积.
答案解析收藏纠错 + 选题
21. (2019八上·徐汇期中) 在平面直角坐标系 $\text{[math]}$ 中（如图），点 $\text{[math]}$ 为直线 $\text{[math]}$ 和双曲线 $\text{[math]}$ 的一个交点，
1. （1）求k、m的值；
2. （2）若点 $\text{[math]}$ ，在直线y=kx上有一点 $\text{[math]}$ ，使得 $\text{[math]}$ ，请求出点 $\text{[math]}$ 的坐标；
3. （3）在双曲线是否存在点 $\text{[math]}$ ，使得 $\text{[math]}$ ，若存在，请求出点 $\text{[math]}$ 的坐标；若不存在请说明理由。
答案解析收藏纠错 + 选题
22. (2019八上·长宁期中) 如图，正方形OAPB、ADFE的顶点A、D．B在坐标轴上，点B在AP上，点P、F在函数 $\text{[math]}$ 上，已知正方形OAPB的面积是9.
1. （1）求k的值和直线OP的解析式；
2. （2）求正方形ADFE的边长
3. （3）函数 $\text{[math]}$ 在第三象限的图像上是否存在一点Q，使得△ABQ的面积为10.5？若存在，求出Q点坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
23. (2019八下·南浔期末) 如图1，在平面直角坐标系xOy中，已知△ABC，∠ABC=90°，顶点A在第一象限内，BC在x轴的正半轴上(B在C的右侧)，AB= $\text{[math]}$ ，∠ACB=30°，△ADC与△ABC关于AC所在的直线对称，且函数y= $\text{[math]}$ (k>0)的图象过点D．
1. （1）当OC=2时，求k的值；
2. （2）如图2，若点A和点D在同一个反比例函数图象上，求OC的长；
3. （3）在(2)的条件下，点D与点E关于原点成中心对称，x轴上有一点F，平面内有一点G，若D、E、F、G四点构成的四边形是矩形，求F点的坐标．
答案解析收藏纠错 + 选题
24. (2019八下·莲都期末) 小明在学习反比例函数后，为研究新函数 $\text{[math]}$ ，先将函数变形为 $\text{[math]}$ ，画图发现函数 $\text{[math]}$ 的图象可以由函数 $\text{[math]}$ 的图象向上平移1个单位得到.
1. （1）根据小明的发现，请你写出函数 $\text{[math]}$ 的图象可以由反比例函数 $\text{[math]}$ 的图象经过怎样的平移得到；
2. （2）在平面直角坐标系中，已知反比例函数 $\text{[math]}$ (x＞0)的图象如图所示，请在此坐标系中画出函数 $\text{[math]}$ (x＞0)的图象；
3. （3）若直线y=－x＋b与函数 $\text{[math]}$ (x＞0)的图象没有交点，求b的取值范围.
答案解析收藏纠错 + 选题
25. (2019八下·长兴期末) 如图，四边形ABCD的四个顶点分别在反比例函数y= $\text{[math]}$ 与y= $\text{[math]}$ (x>0，0<m<n)的图象上，对角线BD∥y轴，且BD⊥AC于点P，已知点B的横坐标为5。
1. （1）当m=10，n=30时
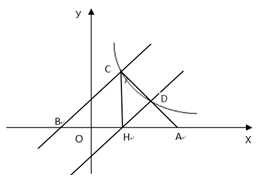
  ①若点P的纵坐标为4，求直线AB的函数表达式
  
  ②若点P是BD的中点，试判断四边形ABCD的形状，并说明理由。
2. （2）四边形ABCD能否成为正方形?若能，求此时m，n之间的数量关系；若不能，试说明理由。
答案解析收藏纠错 + 选题

试卷信息