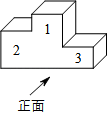
 B .
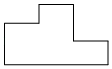
B . 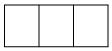 C .
C . 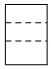 D .
D . 




抽取七年级菜圃的评分(单位:分):
6,6,7,6,6,7,9,7,9,7,9,9,7,9,9,10,9,9,9,10.
抽取八年级菜圃的评分(单位:分):
8,8,7,7,9,9,7,7,7,9,9,7,7,7,8,8,8,9,9,10.
[七、八年级抽取的菜圃评分统计]
年级 | 平均数 | 中位数 | 众数 | 方差 |
七年级 | 8 | a | 9 | 2.65 |
八年级 | 8 | 8 | b | c |

根据以上信息,解答下列问题:

① 若∠BAC=60°,判断以O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;
② 若 , 且AB=20,求OP的长.
若二次函数y=x+2x-3和y=-x-4x-3是同源二次函数,求它们的根函数;
①求满足二次函数C的所有二次函数的根函数;
②若二次函数C与直线x=-3交于点P,求点P到x轴的最小距离,请求出此时m为何值?并求出点P到x轴的最小距离;
数学实践活动,是一种非常有效的学习方式.通过活动可以激发我们的学习兴趣,提高动手动脑能力,拓展思推空间,丰富数学体验.让我们一起动手来折一折、转一转、剪一剪,体会活动带给我们的乐趣.
折一折:将正方形纸片ABCD折叠,使边AB、AD都落在对角线AC上,展开得折痕AE、AF , 连接EF , 如图1.
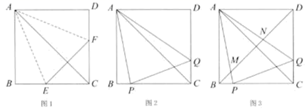
线段BP、PQ、DQ之间的数量关系为;
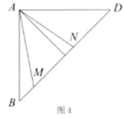
求证: .