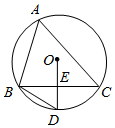



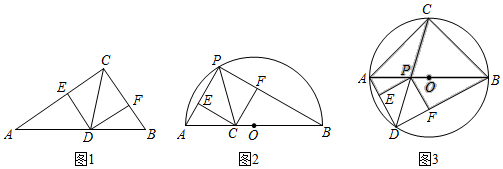
如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是.
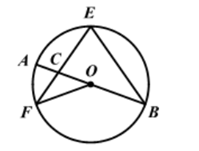
如图2,AB是半圆O的直径,AB=8.P是 上一点,且
,连接AP,BP.∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长.
如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).
①求y与x之间的函数关系式;
②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.
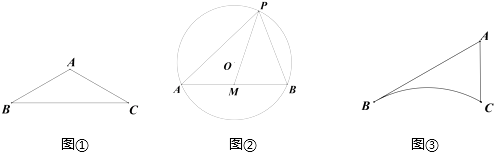
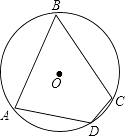
如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为.
如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在弧 BC 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
如图①,△ABC是等边三角形,AB=12,若点O是△ABC的内心,则OA的长为;
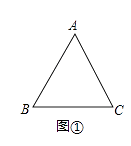
如图②,在矩形ABCD中,AB=12,AD=18,如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由.
某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌.)同时,再合理设计好喷灌龙头喷水的射程就可以了.
如图③,已测出AB=24m,MB=10m,△AMB的面积为96m2;过弦AB的中点D作DE⊥AB交 于点E,又测得DE=8m.
请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)
