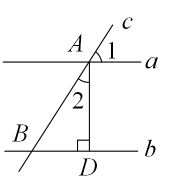




解:∵PN⊥OB于点N,
∴∠PNB= ▲ °( )(填推理的依据).
∵PM∥OB,
∴∠MPN=∠PNB=90°,
∠POB= ▲ ( )(填推理的依据).
∵OP平分∠AOB,且∠AOB=60°,
∴∠POB=∠AOB=30°(角的平分线的定义).
∴∠MPO= ▲ °.
∵∠MPO+∠OPN=∠MPN,
∴∠OPN= ▲ °.

求证: .
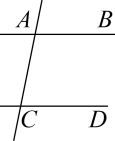
证明:∵DE∥BA
∴ ▲ = ▲ ( )
∵DF∥CA
∴ ▲ = ▲ ( )
∴
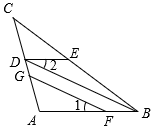
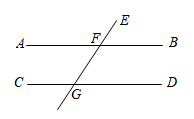
证明:∵BD∥GF( )
∴∠1= ▲ (两直线平行,同位角相等)
∵∠1=∠2(已知)
∴∠2= ▲ ( )
∴DE∥AB( )
∴∠DEC=∠ABC( )
已知:如图,点、
分别在线段
、
上,
,
,
交
于点
,
平分
.
求证:平分
.

证明:∵平分
(已知).
∴(角平分线的定义).
∵(已知),
∴( ).
∴(等量代换).
∵(已知),
∴( ).
▲ (两直线平行,内错角相等).
∴( ).
∴平分
(角平分线的定义).
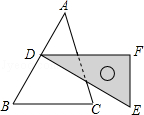
如图1,△ABC中的三个内角分别为∠1,∠2,∠3.将∠2和∠3撕下,按图2的方式拼摆,使∠2和∠3的顶点均与∠1的顶点重合,∠2的一边与AB重合,∠3的一边与AC重合.
|
理由:由操作可知∠B=∠2,
所以AD∥ ▲ (依据: ▲ ).
同理,∠C=∠3,
所以, ▲ ∥ ▲ ,
所以,AD、AE在同一直线上,
所以,∠DAE= ▲ ° ,
即 ∠1+ ▲ + ▲ = ▲ .