苏科版数学2022-2023学年九年级上册一元二次方程单元...

更新时间：2022-10-19 浏览次数：54 类型：单元试卷

一、单选题（每题4分，共40分）

1. (2022九上·定海月考) 将一元二次方程 $\text{[math]}$ 化为一般形式后，其中二次项系数、一次项系数、常数项分别是（）

A . 3，5，-1 B . -3，5，1 C . 3，-5，-1 D . 3，-5，13

答案解析收藏纠错 + 选题
2. (2022九上·恩施月考) 若关于x的一元二次方程 $\text{[math]}$ 有两个不相等实根，则k的取值范围是（　　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 且 $\text{[math]}$ D . $\text{[math]}$ 且 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·寿光期中) 某机械厂七月份生产零件100万个，第三季度生产零件392万个．设该厂八、九月份平均每月的增长率为x，那么x满足的方程是（）

A . 100（1+x）²＝392 B . 100+100（1+x）²＝392 C . 100+100（1+x）+100（1+2x）＝392 D . 100+100（1+x）+100（1+x）²＝392

答案解析收藏纠错 + 选题
4. (2021九上·盐湖月考) 已知等腰△ABC的两边分别是方程x²-10x+21=0的两个根，则△ABC的周长为（）

A . 17 B . 13 C . 11 D . 13或17

答案解析收藏纠错 + 选题
5. (2021九上·沈河期末) 在一次篮球邀请赛中，参赛的每两个队之间都要赛一场，共赛45场，设共有x个队参赛、根据题意可列方程为（）

A . $\text{[math]}$ B . x（x﹣1）＝45 C . $\text{[math]}$ D . x（x+1）＝45

答案解析收藏纠错 + 选题
6. (2022九上·碑林月考) 设 $\text{[math]}$ ， $\text{[math]}$ 是方程 $\text{[math]}$ 的两个实数根，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022九上·通榆月考) 如表是代数式ax²+bx的值的情况，根据表格中的数据，可知方程ax²+bx=6的根是（）
x
……
-3
-2
-1
0
1
2
3
4
……
ax²+bx
……
12
6
2
0
0
2
6
12
……

A . x₁=0，x₂=1 B . x₁=-1，x₂=2 C . x₁=-2，x₂=3 D . x₁=-3，x₂=4

答案解析收藏纠错 + 选题
8. (2022·舟山开学考) 如图，将图1的正方形剪成四块，恰能拼成图2的矩形，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022九上·南宁开学考) 如图，在△ABC中，AB＝AC＝6，∠BAC＝120°，过点A作AD⊥BA交BC于点D，过点D作DE⊥BC交AC于点E，则AE的长为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
10. (2021九上·太原期中) 如图，在活动课上，老师画出边长为2的正方形ABCD ，让同学们按以下步骤完成画图：
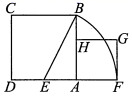
⑴画出AD的中点E ，连接BE；

⑵以点E为圆心，EB长为半径画弧，交DA的延长线于点F；

⑶以AF为边画正方形AFGH ，点H在AB边上．在画出的图中有一条线段的长是方程x²+2x﹣4＝0的一个根．这条线段是（）

A . 线段BH B . 线段BE C . 线段AE D . 线段AH

答案解析收藏纠错 + 选题

二、填空题（每题5分，共25分）

11. (2022九上·龙亭月考) 已知x²－6x+8＝0的两个根分别是等腰三角形的底和腰，则这个三角形的面积是．

答案解析收藏纠错 + 选题
12. (2022八下·东营期末) 如图，在宽为20m，长为32m的矩形地面上修筑同样宽的道路，余下的部分种上草坪，要使草坪的面积为540m² ，求道路的宽若设道路宽为xm，则根据题意可列方程为

答案解析收藏纠错 + 选题
13. (2022九上·榆林月考) “新冠肺炎”防治取得战略性成果，若有一个人患了“新冠肺炎”，经过两轮传染后共有25个人患了“新冠肺炎”，则每轮传染中平均一个人传染了人．

答案解析收藏纠错 + 选题
14. (2021九上·兴文期中) 有一张矩形纸板，长为80cm，宽为60cm，在它的四角各减去一个相同的小正方形；然后折叠成一个无盖的长方形纸盒．若纸盒的底面积（图中阴影部分）为 $\text{[math]}$ ，剪去的小正方形的边长为．

答案解析收藏纠错 + 选题
15. (2021九上·灌阳期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 从点 $\text{[math]}$ 开始沿 $\text{[math]}$ 边向点C以 $\text{[math]}$ 的速度移动，同时另一个点 $\text{[math]}$ 从点C开始沿 $\text{[math]}$ 以 $\text{[math]}$ 的速度移动，当△PCQ的面积等于450m²时，经过的时间是.

答案解析收藏纠错 + 选题

三、综合题（共7题，共85分）

16. (2022九上·应城月考) 用适当的方法解下列一元二次方程：
1. （1） $\text{[math]}$ （用配方法解）
2. （2） $\text{[math]}$
3. （3） $\text{[math]}$
4. （4） $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2022·无为模拟) 某花卉生产基地举行花卉展览，如图所示是用这两种花卉摆成的图案，白色圆点为盆景，灰色圆点为盆花．图1中盆景数量为2，盆花数量为2；图2中盆景数量为4，盆花数量为6；图3中盆景数量为6，盆花数量为12……
按照以上规律，解决下列问题：
1. （1）图6中盆景数量为，盆花数量为；
2. （2）已知该生产基地展出以上两种花卉在某种图案中的数量之和为130盆，分别求出该图案中盆景和盆花的数量；
3. （3）若有n（n为偶数，且 $\text{[math]}$ ）盆盆景需要展出（只摆一种图案），照此组合图案，需要盆花的数量为．（用含n的代数式表示）
答案解析收藏纠错 + 选题
18. (2022九上·福州开学考) 如图，在足够大的空地上有一段长为a米的旧墙，农场决定利用旧墙和篱笆围成中间隔有一道篱笆的矩形菜园ABCD，其中AD≤a，已知矩形菜园的一边靠墙，共用了60米篱笆．
1. （1）若a＝20，所围成的矩形菜园的面积为225平方米，求所利用旧墙AD的长；
2. （2）求矩形菜园ABCD面积的最大值．
答案解析收藏纠错 + 选题
19. (2021八下·慈溪期中) 关于x的一元二次方程x²﹣3x+k＝0有实数根．
1. （1）求k的取值范围；
2. （2）如果k是符合条件的最大整数，且一元二次方程（m﹣1）x²+x+m﹣3＝0与方程x²﹣3x+k＝0有一个相同的根，求此时m的值．
答案解析收藏纠错 + 选题
20. (2022八下·鄞州期中) “阳光玫瑰”葡萄品种是广受各地消费者的青睐的优质新品种，在我国西部区域广泛种植，某葡萄种植基地2018年种植“阳光玫瑰”100亩，到2020年“阳光玫瑰”的种植面积达到256亩.
1. （1）求该基地这两年“阳光攻瑰”种植面积的平均年增长率，
2. （2）市场调查发现，当“阳光玫瑰”的售价为20元/千克时，每天能售出200千克，售价每降价1元，每天可多售出45千克.
  ①若降价x（0≤x≤20）元，每天能售出多少千克？（用x的代数式表示）
  
  ②为了推广宣传，基地决定降价促销，同时尽量减少库存，已知该基地“阳光玫瑰”的平均成本价为10元/千克，若要销售“阳光玫瑰”每天获利2125元，则售价应降低多少元？
答案解析收藏纠错 + 选题
21. (2022八下·义乌期中) 如图，四边形ACDE是证明勾股定理时用到的一个图形，a，b，c是Rt△ABC和Rt△BED边长，易知AE＝ $\text{[math]}$ c，这时我们把关于x的形如ax²+ $\text{[math]}$ cx+b＝0的一元二次方程称为“勾系一元二次方程”．
请解决下列问题：
1. （1）试判断方程 $\text{[math]}$ 是否为 “勾系一元二次方程”；
2. （2）求证：关于x的“勾系一元二次方程”ax²+ $\text{[math]}$ cx+b＝0必有实数根；
3. （3）若x＝﹣1是“勾系一元二次方程”ax²+ $\text{[math]}$ cx+b＝0的一个根，且四边形ACDE的周长是12，求△ABC面积．
答案解析收藏纠错 + 选题
22. (2022九上·宿豫开学考) 我们知道： $\text{[math]}$ ； $\text{[math]}$ ，这一种方法称为配方法，利用配方法请解以下各题：
1. （1）按上面材料提示的方法填空： $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ．
2. （2）探究：当 $\text{[math]}$ 取不同的实数时在得到的代数式 $\text{[math]}$ 的值中是否存在最小值？请说明理由．
3. （3）应用：如图．已知线段 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上的一个动点，设 $\text{[math]}$ ，以 $\text{[math]}$ 为一边作正方形 $\text{[math]}$ ，再以 $\text{[math]}$ 、 $\text{[math]}$ 为一组邻边作长方形 $\text{[math]}$ 问：当点 $\text{[math]}$ 在 $\text{[math]}$ 上运动时，长方形 $\text{[math]}$ 的面积是否存在最大值？若存在，请求出这个最大值；否则请说明理由．
答案解析收藏纠错 + 选题