2023中考数学真题复习第01讲规律探索类

更新时间：2022-11-03 浏览次数：138 类型：一轮复习

一、单选题（每题2分，共18分）

1. (2024八下·昂仁期中) 按一定规律排列的一组数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …．则按此规律排列的第10个数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·鄂州) 生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型.在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2ⁿ来表示.即：2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，……，请你推算2²⁰²²的个位数字是（）

A . 8 B . 6 C . 4 D . 2

答案解析收藏纠错 + 选题
3. (2023·重庆市模拟) 把菱形按照如图所示的规律拼图案，其中第①个图案中有 1个菱形，第②个图案中有 3个菱形，第③个图案中有5个菱形，…，按此规律排列下去，则第⑥个图案中菱形的个数为（）

A . 15 B . 13 C . 11 D . 9

答案解析收藏纠错 + 选题
4. (2022·重庆) 用正方形按如图所示的规律拼图案，其中第①企图案中有5个正方形，第②个图案中有9个正方形，第③全图案中有13全正方形，第④个图案中有17企正方形，此规律排列下去，则第⑨个图案中正方形的个数为（）

A . 32 B . 34 C . 37 D . 41

答案解析收藏纠错 + 选题
5. (2022·新疆) 将全体正偶数排成一个三角形数阵：
按照以上排列的规律，第10行第5个数是（）

A . 98 B . 100 C . 102 D . 104

答案解析收藏纠错 + 选题
6. (2022七上·阳西期末) 如图，用相同的圆点按照一定的规律拼出图形．第一幅图4个圆点，第二幅图7个圆点，第三幅图10个圆点，第四幅图13个圆点……按照此规律，第一百幅图中圆点的个数是（）

A . 297 B . 301 C . 303 D . 400

答案解析收藏纠错 + 选题
7. (2024七下·惠来月考) 如图，用若干根相同的小木棒拼成图形，拼第1个图形需要6根小木棒，拼第2个图形需要14根小木棒，拼第3个图形需要22根小木棒……若按照这样的方法拼成的第n个图形需要2022根小木棒，则n的值为（）

A . 252 B . 253 C . 336 D . 337

答案解析收藏纠错 + 选题
8. (2023·金乡县模拟) 由12个有公共顶点O的直角三角形拼成如图所示的图形，∠AOB＝∠BOC＝∠COD＝…＝∠LOM＝30°．若S△AOB＝1，则图中与△AOB位似的三角形的面积为（）

A . （ $\text{[math]}$ ）³ B . （ $\text{[math]}$ ）⁷ C . （ $\text{[math]}$ ）⁶ D . （ $\text{[math]}$ ）⁶

答案解析收藏纠错 + 选题
9. (2023九上·保定开学考) 如图，在平面直角坐标系中，将边长为2的正六边形 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 个 $\text{[math]}$ ，得到正六边形 $\text{[math]}$ ，当 $\text{[math]}$ 时，正六边形 $\text{[math]}$ 的顶点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每空1分，共4分）

10. (2022七上·鸡西期中) 按一定规律排列的数据依次为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ……按此规律排列，则第30个数是．

答案解析收藏纠错 + 选题
11. (2022·青海) 木材加工厂将一批木料按如图所示的规律依次摆放，则第 $\text{[math]}$ 个图中共有木料根.

答案解析收藏纠错 + 选题
12. (2022·黔西) 如图，在平面直角坐标系中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点为 $\text{[math]}$ ； $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点为 $\text{[math]}$ ； $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点为 $\text{[math]}$ ； $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点为 $\text{[math]}$ ；…；按此做法进行下去，则点 $\text{[math]}$ 的坐标为．

答案解析收藏纠错 + 选题
13. (2022·东营) 如图， $\text{[math]}$ 是等边三角形，直线 $\text{[math]}$ 经过它们的顶点 $\text{[math]}$ ，点 $\text{[math]}$ 在x轴上，则点 $\text{[math]}$ 的横坐标是.

答案解析收藏纠错 + 选题

三、综合题（共13题，共78分）

14. (2022·泰安) 观察下列图形规律，当图形中的“○”的个数和“．”个数差为2022时，n的值为．

答案解析收藏纠错 + 选题
15. (2023七下·东台期中) 古希腊的毕达哥拉斯学派对整数进行了深入的研究，尤其注意形与数的关系，“多边形数”也称为“形数”，就是形与数的结合物.用点排成的图形如下：其中：图①的点数叫做三角形数，从上至下第一个三角形数是1，第二个三角形数是 $\text{[math]}$ ，第三个三角形数是 $\text{[math]}$ ，……图②的点数叫做正方形数，从上至下第一个正方形数是1，第二个正方形数是 $\text{[math]}$ ，第三个正方形数是 $\text{[math]}$ ，……由此类推，图④中第五个正六边形数是.

答案解析收藏纠错 + 选题
16. (2021七上·仙居期中) 如图，将正整数按此规律排列成数表，则2021是表中第行第列.

答案解析收藏纠错 + 选题
17. (2022·大庆模拟) 古希腊数学家把1，3，6，10，15，21，…这样的数叫做三角形数，因为它的规律性可以用如图表示.根据图形，若把第一个图形表示的三角形数记为 $\text{[math]}$ ，第二个图形表示的三角形数记为 $\text{[math]}$ ，…，则第 $\text{[math]}$ 个图形表示的三角形数 $\text{[math]}$ ＝.（用含 $\text{[math]}$ 的式子表达）

答案解析收藏纠错 + 选题
18. (2020·黔南) 在2020年新冠肺炎疫情期间，某中学响应政府有“停课不停学”的号召，充分利用网络资源进行网上学习，九年级1班的全体同学在自主完成学习任务的同时，彼此关怀，全班每两个同学都通过一次电话，互相勉励，共同提高，如果该班共有48名同学，若每两名同学之间仅通过一次电话，那么全同学共通过多少次电话呢？我们可以用下面的方式来解决问题.
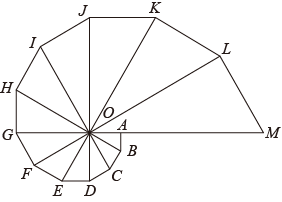
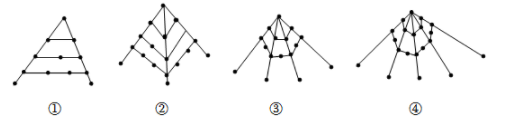
用点A₁、A₂、A₃…A₄₈分表示第1名同学、第2名同学、第3名同学…第48名同学，把该班级人数x与通电话次数y之间的关系用如图模型表示：
1. （1）填写上图中第四个图中y的值为，第五个图中y的值为.
2. （2）通过探索发现，通电话次数y与该班级人数x之间的关系式为，当x＝48时，对应的y＝.
3. （3）若九年级1班全体女生相互之间共通话190次，问：该班共有多少名女生？
答案解析收藏纠错 + 选题
19. (2011·宁波)
用同样大小的黑色棋子按如图所示的规律摆放：
1. （1）第5个图形有多少黑色棋子？
2. （2）第几个图形有2013颗黑色棋子？请说明理由．
答案解析收藏纠错 + 选题
20. (2018·黔西南) “分块计数法”：对有规律的图形进行计数时，有些题可以采用“分块计数”的方法．
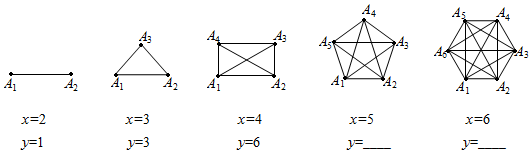
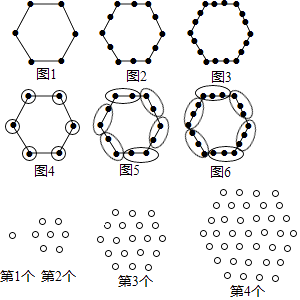
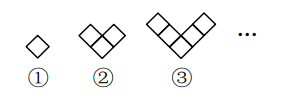
例如：图1有6个点，图2有12个点，图3有18个点，……，按此规律，求图10、图n有多少个点？
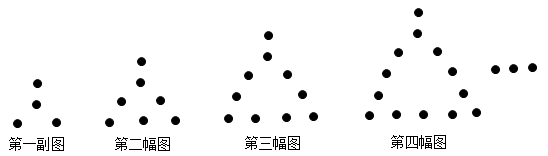
1. （1）我们将每个图形分成完全相同的6块，每块黑点的个数相同（如图），这样图1中黑点个数是6×1=6个；图2中黑点个数是6×2=12个：图3中黑点个数是6×3=18个；所以容易求出图10、图n中黑点的个数分别是、．
2. （2）请你参考以上“分块计数法”，先将下面的点阵进行分块（画在答题卡上），再完成以下问题：
  ①第5个点阵中有个圆圈；第n个点阵中有个圆圈．
  ②小圆圈的个数会等于271吗？如果会，请求出是第几个点阵．
答案解析收藏纠错 + 选题
21. (2024九上·石家庄期末) 设 $\text{[math]}$ 是一个两位数，其中a是十位上的数字（1≤a≤9）．例如，当a＝4时， $\text{[math]}$ 表示的两位数是45．
1. （1）尝试：
  ①当a＝1时，15²＝225＝1×2×100＋25；
  
  ②当a＝2时，25²＝625＝2×3×100＋25；
  
  ③当a＝3时，35²＝1225＝；
  
  ……
2. （2）归纳： $\text{[math]}$ 与100a(a＋1)＋25有怎样的大小关系？试说明理由．
3. （3）运用：若 $\text{[math]}$ 与100a的差为2525，求a的值．
答案解析收藏纠错 + 选题
22. 观察以下等式：
第1个等式： $\text{[math]}$ ，
第2个等式： $\text{[math]}$ ，
第3个等式： $\text{[math]}$ ，
第4个等式： $\text{[math]}$ ，
……
按照以上规律．解决下列问题：
1. （1）写出第5个等式：；
2. （2）写出你猜想的第n个等式（用含n的式子表示），并证明．
答案解析收藏纠错 + 选题
23. 观察下面的等式： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，……
1. （1）按上面的规律归纳出一个一般的结论(用含n的等式表示，n为正整数)．
2. （2）请运用分式的有关知识，推理说明这个结论是正确的。
答案解析收藏纠错 + 选题
24. (2022·和县模拟) 观察以下等式：
第1个等式： $\text{[math]}$

第 $\text{[math]}$ 个等式： $\text{[math]}$

第3个等式： $\text{[math]}$

第 $\text{[math]}$ 个等式： $\text{[math]}$

第5个等式： $\text{[math]}$

······

按照以上规律．解决下列问题：
1. （1）写出第6个等式；
2. （2）写出你猜想的第n个等式：(用含n的等式表示)，并证明．
答案解析收藏纠错 + 选题
25. (2020八上·芜湖期末) 观察下列各个等式的规律：
第一个等式： $\text{[math]}$ =1，第二个等式： $\text{[math]}$ =2，第三个等式： $\text{[math]}$ =3…
请用上述等式反映出的规律解决下列问题：
1. （1）直接写出第四个等式；
2. （2）猜想第n个等式（用n的代数式表示），并证明你猜想的等式是正确的．
答案解析收藏纠错 + 选题
26. (2017·内江) 观察下列等式：
第一个等式： $\text{[math]}$
第二个等式： $\text{[math]}$
第三个等式： $\text{[math]}$
第四个等式： $\text{[math]}$
按上述规律，回答下列问题：
1. （1）请写出第六个等式：a₆==；
2. （2）用含n的代数式表示第n个等式：a_n==；
3. （3） a₁+a₂+a₃+a₄+a₅+a₆=（得出最简结果）；
4. （4）计算：a₁+a₂+…+a_n ．
答案解析收藏纠错 + 选题