浙教版备考2023年中考数学一轮复习42.二次函数与一次函数

更新时间：2022-12-25 浏览次数：110 类型：一轮复习

一、单选题（每题3分，共30分）

1. (2022九上·定海期中) 在平面直角坐标系xOy中，已知点M，N的坐标分别为（-1，2），（2，1），若抛物线 $\text{[math]}$ （a≠0）与线段MN有两个不同的交点，则a的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022九上·通州月考) 抛物线y1=（x﹣2）²﹣1与直线y₂=x﹣1交于A、B两点，则当y₂≥y₁时，x的取值范围为（）

A . 1≤x≤4 B . x≤4 C . x≥1 D . x≤1或x≥4

答案解析收藏纠错 + 选题
3. (2021九上·南宁期中) 一次函数 $\text{[math]}$ 与二次函数 $\text{[math]}$ 在同一平面直角坐标系中的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022九上·长沙开学考) 在平面直角坐标系内，已知点 $\text{[math]}$ ，点 $\text{[math]}$ 都在直线 $\text{[math]}$ 上，若抛物线 $\text{[math]}$ 与线段 $\text{[math]}$ 有两个不同的交点，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ 成 $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022九上·鄞州开学考) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022九上·瑞安期中) 如图，将抛物线 $\text{[math]}$ 沿 $\text{[math]}$ 轴翻折，翻折前后的两条抛物线构成一个新图象．若直线 $\text{[math]}$ 与这个新图象有3个公共点，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ 或2 B . $\text{[math]}$ 或2 C . 2或4 D . $\text{[math]}$ 或4

答案解析收藏纠错 + 选题
7. (2022九上·杭州月考) 如图，抛物线y＝﹣2x²+8x﹣6与x轴交于点A、B，把抛物线在x轴及其上方的部分记作C₁ ，将C₁向右平移得C₂ ， C₂与x轴交于点B，D．若直线y＝x+n与C₁、C₂共有3个不同的交点，则n的取值范围是（）

A . $\text{[math]}$ ＜n＜ $\text{[math]}$ B . $\text{[math]}$ ＜n＜ $\text{[math]}$ C . $\text{[math]}$ ＜n＜ $\text{[math]}$ D . $\text{[math]}$ ＜n＜ $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022九上·宁波期中) 如图，“心”形是由抛物线 $\text{[math]}$ 和它绕着原点O，顺时针旋转60°的图形经过取舍而成的，其中顶点C的对应点为D，点A，B是两条抛物线的两个交点，直线AB为“心”形对称轴，点E，F，G 是抛物线与坐标轴的交点，则AB=（）

A . $\text{[math]}$ B . 8 C . 10 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 如图，抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于A、B两点，下列是关于x的不等式或方程，结论正确的是（）

A . $\text{[math]}$ 的解集是 $\text{[math]}$ B . $\text{[math]}$ 的解集是 $\text{[math]}$ C . $\text{[math]}$ 的解集是 $\text{[math]}$ D . $\text{[math]}$ 的解是 $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022九上·长沙开学考) 已知二次函数 $\text{[math]}$ 下列结论正确是（）
①已知点 $\text{[math]}$ ，点 $\text{[math]}$ 在二次函数的图象上，则 $\text{[math]}$ ；②该图象一定过定点 $\text{[math]}$ 和 $\text{[math]}$ ；③直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 一定存在两个交点；④当 $\text{[math]}$ 时， $\text{[math]}$ 的最小值是 $\text{[math]}$ ，则 $\text{[math]}$ ；

A . ①④ B . ②③ C . ②④ D . ①②③④

答案解析收藏纠错 + 选题

二、填空题（每空3分，共21分）

11. (2024九下·潜山模拟) 定义：min{a，b}＝ $\text{[math]}$ 若函数y＝min{x＋1， $\text{[math]}$ }，则该函数的最大值为.

答案解析收藏纠错 + 选题
12. (2023九上·天河期中) 已知二次函数y＝﹣x²+bx+c与一次函数y＝mx+n的图象相交于点A（﹣2，4）和点B（6，﹣2），则不等式﹣x²+bx+c＞mx+n的解集是．

答案解析收藏纠错 + 选题
13. (2021九上·青浦期末) 如图，一次函数 $\text{[math]}$ 的图像与x轴，y轴分别相交于点A，点B，将它绕点O逆时针旋转90°后，与x轴相交于点C，我们将图像过点A，B，C的二次函数叫做与这个一次函数关联的二次函数．如果一次函数 $\text{[math]}$ 的关联二次函数是 $\text{[math]}$ （ $\text{[math]}$ ），那么这个一次函数的解析式为．

答案解析收藏纠错 + 选题
14. (2022九上·海珠期中) 抛物线 $\text{[math]}$ 的图象为 $\text{[math]}$ ， $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的图象为 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 组成的图象与直线 $\text{[math]}$ 有3个公共点时， $\text{[math]}$ 的范围（或值）是．

答案解析收藏纠错 + 选题
15. (2022·湘西) 已知二次函数y＝﹣x²+4x+5及一次函数y＝﹣x+b，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新图象（如图所示），当直线y＝﹣x+b与新图象有4个交点时，b的取值范围是．

答案解析收藏纠错 + 选题
16. (2022·金东模拟) 一个玻璃杯竖直放置时的纵向截面如图1所示，其左右轮廓线 $\text{[math]}$ ， $\text{[math]}$ 为同一抛物线的一部分， $\text{[math]}$ ， $\text{[math]}$ 都与水平地面平行，当杯子装满水后 $\text{[math]}$ ， $\text{[math]}$ ，液体高度 $\text{[math]}$ ，将杯子绕 $\text{[math]}$ 倾斜倒出部分液体，当倾斜角 $\text{[math]}$ 时停止转动，如图2所示，此时液面宽度 $\text{[math]}$ $\text{[math]}$ ，液面 $\text{[math]}$ 到点 $\text{[math]}$ 所在水平地面的距离是 $\text{[math]}$ ．

图1 图2

答案解析收藏纠错 + 选题

三、解答题（共8题，共69分）

17. (2023九上·东光月考) 已知二次函数 $\text{[math]}$ 的图象与x轴交于A、B两点（A在B的左侧），与y轴交于点C，顶点为D.
1. （1）求点A、B、D的坐标，并在下面直角坐标系中画出该二次函数的大致图象；
2. （2）设一次函数 $\text{[math]}$ 的图象经过B、C两点，请直接写出满足 $\text{[math]}$ 的x的取值范围.
答案解析收藏纠错 + 选题
18. (2021九上·白云期中) 如图，已知二次函数y＝﹣x²+2x+3图象与x轴的其中一个交点为A，与y轴交于点B，若直线AB与这个二次函数图象的对称轴交于点P，求点P的坐标．

答案解析收藏纠错 + 选题
19. (2022九上·杭州期中) 已知二次函数 $\text{[math]}$ 的图象与直线 $\text{[math]}$ 交于点A（-1，0）、点C（4，m）.
1. （1）求 $\text{[math]}$ 的表达式和m的值；
2. （2）当 $\text{[math]}$ 时，求自变量x的取值范围；
3. （3）将直线AC沿y轴上下平移，当平移后的直线与抛物线只有一个公共点时，求平移后的直线表达式.
答案解析收藏纠错 + 选题
20. (2022九上·拱墅月考) 在平面直角坐标系内，二次函数y₁＝（x﹣a）²+a﹣1（a为常数）．
1. （1）若函数y的图象经过点（1，0），求函数y₁的表达式．
2. （2）若y₁的图象与一次函数y₂＝x+1的图象有两个交点，横坐标分别为﹣1，2，请直接写出当y₁＞y₂时x的取值范围．
3. （3）已知（x₀ ， n）在函数y₁的图象上，当x₀＞2a＞0时，求证：n＞﹣ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2022九上·晋安月考) 已知抛物线y＝x²+bx+c与x轴交于点A（1﹣m，0），B（1+m，0）.点A在点B的左侧，且与y轴交于点C（0，﹣3）.
1. （1）求这条抛物线的解析式；
2. （2）已知D为该抛物线的顶点，E为抛物线第四象限上一点，若过点E的直线l与直线BD关于直线y＝﹣x对称.
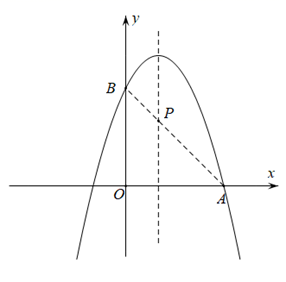
  ①求点E的坐标；
  ②直线y＝2kx+k﹣ $\text{[math]}$ （k＞0）与这条抛物线交于点M，N，连接ME，NE，判断ME，NE，MN之间的数量关系，并说明理由.
答案解析收藏纠错 + 选题

22. (2022·武汉) 在一条笔直的滑道上有黑、白两个小球同向运动，黑球在 $\text{[math]}$ 处开始减速，此时白球在黑球前面 $\text{[math]}$ 处.

小聪测量黑球减速后的运动速度 $\text{[math]}$ （单位： $\text{[math]}$ ）、运动距离 $\text{[math]}$ （单位： $\text{[math]}$ ）随运动时间 $\text{[math]}$ （单位： $\text{[math]}$ ）变化的数据，整理得下表.

运动时间 $\text{[math]}$	0	1	2	3	4
运动速度 $\text{[math]}$	10	9.5	9	8.5	8
运动距离 $\text{[math]}$	0	9.75	19	27.75	36

小聪探究发现，黑球的运动速度 $\text{[math]}$ 与运动时间 $\text{[math]}$ 之间成一次函数关系，运动距离 $\text{[math]}$ 与运动时间 $\text{[math]}$ 之间成二次函数关系.

（1）直接写出 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式和 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式（不要求写出自变量的取值范围）
（2）当黑球减速后运动距离为 $\text{[math]}$ 时，求它此时的运动速度；
（3）若白球一直以 $\text{[math]}$ 的速度匀速运动，问黑球在运动过程中会不会碰到白球？请说明理由.

答案解析收藏纠错 + 选题

23. (2022九上·义乌期中) 阅读材料：一般地，对于某个函数，如果自变量x在取值范围内任取x＝a与x＝ $\text{[math]}$ 时，函数值相等，那么这个函数是“对称函数”.例如，y＝x² ，在实数范围内任取x＝a时，y＝a²；当x＝ $\text{[math]}$ 时，y＝ $\text{[math]}$ ＝ a² ，所以y＝x²是“对称函数”.
1. （1）函数 $\text{[math]}$ 对称函数（填“是”或“不是”）.当x≥0时， $\text{[math]}$ 的图象如图1所示，请在图1中画出x＜0时， $\text{[math]}$ 的图象.
2. （2）函数 $\text{[math]}$ 的图象如图2所示，当它与直线y＝－x+n恰有3个交点时，求n的值.
3. （3）如图3，在平面直角坐标系中，矩形ABCD的顶点坐标分别是A（－3，0），B（2，0），C（2，－3），D（－3，－3），当二次函数 $\text{[math]}$ （b>0）的图象与矩形的边恰有4个交点时，求b的取值范围.
答案解析收藏纠错 + 选题
24. (2022·宜昌) 已知抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ .直线 $\text{[math]}$ 由直线 $\text{[math]}$ 平移得到，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ .四边形 $\text{[math]}$ 的四个顶点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）填空： $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）若点 $\text{[math]}$ 在第二象限，直线 $\text{[math]}$ 与经过点 $\text{[math]}$ 的双曲线 $\text{[math]}$ 有且只有一个交点，求 $\text{[math]}$ 的最大值；
3. （3）当直线 $\text{[math]}$ 与四边形 $\text{[math]}$ 、抛物线 $\text{[math]}$ 都有交点时，存在直线 $\text{[math]}$ ，对于同一条直线 $\text{[math]}$ 上的交点，直线 $\text{[math]}$ 与四边形 $\text{[math]}$ 的交点的纵坐标都不大于它与抛物线 $\text{[math]}$ 的交点的纵坐标.
  ①当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的取值范围；
  
  ②求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题